Общее уравнение Шредингера. Уравнение Шредингера

Для стационарных состояний

Статистическое толкование волн де Бройля и соотношение неопределенностей Гейзенберга привели к выводу что уравнением движения в квантовой механике, описывающем движение микрочастиц в различных силовых полях, должно быть уравнение, из которого бы вытекали наблюдаемые на опыте волновые свойства частиц. Основное уравнение должно было быть уравнением относительно волновой функции 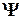(х, у, z, t), т.к. именно она или, точнее, величина 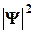определяет вероятность пребывания частицы в момент времени t в объеме dV, т.е. в области с координатами х и х + dx, у и у + dy, z и z +

Dz.

Так как искомое уравнение должно учитывать волновые свойства частиц, то оно должно быть волновым уравнением, подобно уравнению, описывающему электромагнитные волны.

Основное уравнение нерелятивистской квантовой механики сформулировано в 1926 г. Э. Шредингером. Оно, как и все основные уравнения физики (например, уравнения Ньютона в классической механике и уравнения Максвелла для электромагнитного поля), не выводится, а постулируется. Правильность подтверждается согласием с опытом получаемых с его помощью результатов, что, в свою очередь, придает ему

характер закона природы. Уравнение Шредингера имеет вид

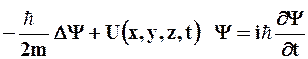, (8.9)

где 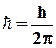; m – массачастицы; 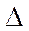- оператор Лапласа

;

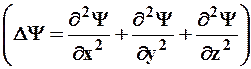U (х, у, z, t) - потенциальная функция частицы в силовом поле, в котором она движется: 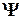(х, у, z, t) - искомая волновая функция частицы; i -мнимая единица.

Уравнение (8.9) справедливо для любой частицы, движущейся с малой скоростью, т.е. со скоростью v<<с, и дополняется условиями, накладываемыми на волновую функцию: 1) конечность, однозначность и непрерывность; 2) производные

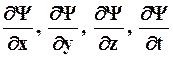
должны быть непрерывны; 3) функция 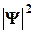должна быть интегрируема (это условие в простейших случаях сводится к условию нормировки вероятностей).

Уравнение (8.9) является общим уравнением Шредингера или уравнением, зависящим от времени. Для многих физических явлений, происходящих в микромире, уравнение (8.9) можно упростить, исключив зависимость 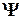от времени. Иными словами, найти уравнение Шредингера для стационарных состояний, т.е. с фиксированными значениями энергии. Это возможно, если силовое поле, в котором частица движется, стационарно, т.е. функция U = U (x,y,z) не зависит явно от времени и имеет смысл потенциальной энергии. В данном случае решение уравнения Шредингера может быть представлено в виде произведения двух функций, одна из которых есть функция только координат, другая - только времени.

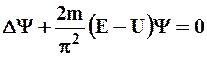. (8.10)

Уравнение (8.10) называется уравнением Шредингера для стационарных состояний.

В это уравнение в качестве параметра входит полная энергия Е частицы. В теории дифференциальных уравнений доказывается, что подобные уравнения имеют бесчисленное множество решений, из которых посредством наложения граничных условий отбирают имеющие физический смысл. Для уравнения Шредингера такими являются условия регулярности волновых функций: конечность, однозначность и непрерывность вместе со своими первыми производными. Таким образом, реальный физический смысл имеют только такие решения, которые выражаются регулярными функциями 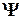. Но регулярные решения имеют место не при любых значениях параметра Е, а лишь при определенном их наборе, характерном для данной задачи. Эти значения энергии называются собственными. Решения же, которые соответствуют собственным значениям энергии, называются собственными функциями. Собственные значения Е могут образовывать как непрерывный, так и дискретный ряд. В первом случае говорят о непрерывном, или сплошном спектре, во втором - о дискретном спектре.

Date: 2015-05-08; view: 509; Нарушение авторских прав