Соотношение неопределенностей

Согласно двойственной корпускулярно-волновой природе частиц вещества, для описания микрочастиц используются то волновые, то корпускулярные представления. Поэтому приписывать им все свойства частиц и все свойства волн нельзя. Естественно, что необходимо внести некоторые ограничения в применении к объектам микромира понятий классической механики.

Микрочастицы из-за наличия у них волновых свойств существенно отличаются от классических: что нельзя говорить о движении их по определенной траектории с точно фиксированными координатой и импульсом в любой момент времени. Это следует из корпускулярно-волнового дуализма. Так, понятие "длина волны в данной точке" лишено физического смысла, а поскольку импульс выражается через длину волны, то отсюда следует, что микрочастица находится в состоянии с точным значением координаты, то ее импульс является полностью неопределенным.

В. Гейзенберг, учитывая волновые свойства микрочастиц и связанные с ними ограничения в их поведении, пришел в 1927 г. к выводу, что объект микромира невозможно одновременно с любой наперед заданной точностью характеризовать и координатой и импульсом.

Согласно соотношению неопределенностей Гейзенберга, микрочастица (микрообъект) не может иметь одновременно и определенную координату (х, у, z), и определенную соответствующую проекцию импульса (P_x, P _y, P_z), причем неопределенности этих величин удовлетворяют условиям

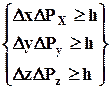, (8.4)

т.е. произведение неопределенностей координаты и соответствующей ей проекции импульса не может быть меньше величины порядка h.

Из соотношения неопределенностей следует, что если микрочастица находится, например, в состоянии с точным значением координаты (Δх =0), то в этом состоянии соответствующая проекция ее импульса оказывается совершенно неопределенной 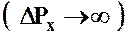и наоборот. Таким образом, для микрочастицы не существует состояния, в котором ее координаты и импульс имели бы одновременно точные значения. Отсюда вытекает и фактическая невозможность одновременно с любой наперёд заданной точностью измерить координаты и импульс микрообъекта, что является следствием объективных свойств, а именно: двойственной корпускулярно-волновой природы. Соотношение неопределенностей получено при одновременном использовании классических характеристик движения частицы (координаты, импульса) и наличия у нее волновых свойств.

Это соотношение, отражая специфику физики микрочастицы, позволяет оценить, например, в какой мере можно применять понятие классической механики к микрочастицам. В частности, с какой степенью точности можно говорить о траекториях микрочастиц. Известно, что движение по траектории характеризуется в любой момент времени определенными значениями координат и скорости. Выразим соотношение неопределенностей (8.4) в виде

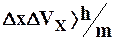. (8.5)

Из этого выражения следует: чем больше масса частиц, тем меньше неопределенности ее координат и скорости и, следовательно, с тем большей точностью можно применять к этой частице понятие траектории. Так, например, уже для пылинки массой 10^-12 кг и линейными размерами 10^-6м, координата которой определена с точностью до 0,01 ее размеров (Dх =10^-8 м), неопределенность скорости, по (8.5), ΔV_x = 6,62×10^-14 м/c, т.е. не будет сказываться при всех скоростях, с которыми пылинка может двигаться. Таким образом, для макроскопических тел их волновые свойства не играют никакой роли; координаты и скорость могут быть одновременно измерены достаточно точно. Это же означает, что для описания движения макротел с абсолютной достоверностью можно пользоваться законами классической механики.

Предположим, пучок электронов движется вдоль оси х со скоростью v = 10⁸ м/с, определяемой с точностью до 0,01 % (ΔV _x 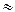10⁴ м/с). Какова точность определения координаты электрона? По формуле (8.5):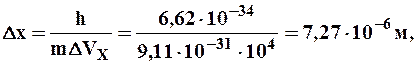

т.е. положение электрона может быть определено с точностью до тысячных долей миллиметра. Такая точность достаточна, чтобы можно было говорить о движении электронов по определенной траектории. Иными словами, описывать их движение законами классической механики.

Применим соотношение неопределенностей к электрону, движущемуся в атоме водорода. Допустим, что неопределенность координаты электрона Δх 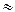10^-10 м (порядка размеров самого атома, т.е. можно считать, что электрон принадлежит данному атому). Тогда, согласно (8.5)

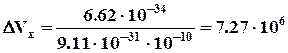м/с.

Используя законы классической физики, можно показать, что при движении электрона вокруг ядра по круговой орбите радиусом»0,5×10^-10 м его скорость u»2,3×10⁶ м/с. Таким образом, неопределенность скорости в несколько раз больше самой скорости. Очевидно, что в данном случае нельзя говорить о движении электрона в атоме по определённой траектории. Иными словами, для описания движения электрона в атоме нельзя пользоваться законами классической физики.

Соотношение неопределенностей в течение длительного времени являлось предметом философских дискуссий, приводивших некоторых философов к его идеалистическому истолкованию. Например, по их мнению, соотношение неопределенностей, не давая возможности одновременно точно определить координаты и импульсы (скорости) частиц, устанавливает границу познаваемости мира, с одной стороны, и существование микрообъектов вне пространства и времени - с другой. На самом деле это понятие не ставит к.-л. предела познанию микромира, а только указывает, насколько применимы к нему определения классической механики.

8.3. Волновая функция и её статистический смысл

Экспериментальное подтверждение идеи де Бройля об универсальности корпускулярно-волнового дуализма, ограниченность применения классической механики к микрообъектам, диктуемая соотношением неопределенностей, а также противоречие целого ряда экспериментов с применяемыми в начале 20 в. теориями привели к новому этапу развития квантовой теории - созданию квантовой механики (1900 – 1920 г.), описывающей законы движения и взаимодействия микрочастиц с учетом их волновых свойств.

Она связана прежде всего с именами австрийского физика Э. Шредингера, немецкого физика В. Гейзенберга и английского физика П. Дирака.

При развитии теории о двойственности природы волн де Бройля возникли новые принципиальные проблемы, в частности проблема их физической природы.

Для выяснения проблемы сравним дифракцию световых волн и микрочастиц. Дифракционная картина, наблюдаемая для световых волн, характеризуется тем, что в результате наложения дифрагирующих волн друг на друга в различных точках пространства происходит деление или ослабление амплитуды колебаний. Согласно волновым представлениям о природе света, интенсивность дифракционной картины пропорциональна квадрату амплитуды световой волны.

По представлениям фотонной теории, интенсивность определяется числом фотонов, попадающих в данную точку дифракционной картины. Следовательно, число фотонов в данной точке дифракционной картины задается квадратом амплитуды световой волны, в то время как для одного фотона квадрат амплитуды определяет вероятность попадания фотона в ту или иную точку.

Математическая связь между квадратом амплитуды и вероятность того, что фотон будет обнаружен в пределах объема dV, заключающего в себе рассматриваемую точку пространства:

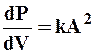
где 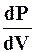- плотность вероятности; к – коэффициент пропорциональности; А – амплитуда световой волны.

Дифракционная картина, наблюдаемая для микрочастиц, также характеризуется неодинаковым распределением потоков микрочастиц, рассеянных или отраженных по различным направлениям – в одних направлениях наблюдается большее число частиц, чем в других. Наличие максимумов в дифракционной картине с точки зрения волновой теории означает, что эти направления соответствуют наибольшей интенсивности волн де Бройля. С другой стороны, интенсивность волн де Бройля оказывается больше там, где имеется большее число частиц. Таким образом, дифракционная картина для микрочастиц является проявлением статистической (вероятностной) закономерности, согласно которой частицы попадают в те места, где интенсивность волн де Бройля наибольшая.

Необходимость вероятностного подхода к описанию микрочастиц является важнейшей отличительной особенностью квантовой теории. Немецкий физик М. Борн предположил, что по закону волновой теории меняется не сама вероятность, а величина, названная амплитудой вероятности (волновой функцией) и обозначаемая 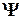(x,y,z).

Амплитуда вероятности может быть комплексной, а вероятность W пропорциональна квадрату ее модуля:

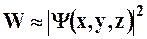. (8.6)

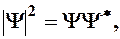
( - функция комплексно сопряженная с 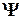). Таким образом, описание состояния микрообъекта с помощью волновой функции имеет статистический, вероятностный характер: квадрат модуля волновой функции (квадрат модуля амплитуды волн де Бройля) определяет вероятность нахождения частицы в момент времени t в области с координатами x и x+dx, y и y+dy, z и z+dz.

Итак, в квантовой механике состояние микрочастиц описывается принципиально по-новому - с помощью волновой функции, которая является основным носителем информации об их корпускулярных и волновых свойствах.

Вероятность нахождения частицы в элементе объемом dv равна

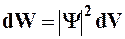. (8.7)

Date: 2015-05-08; view: 910; Нарушение авторских прав