Квантование энергии

Уравнение Шредингера позволяет решать практические задачи и находить состояния движения частиц в различных внешних полях.

Электрические свойства металлов объясняются наличием в них свободных электронов. Результирующая сила, действующая на электрон со стороны ионов и всех остальных электронов, в среднем равна нулю. Следовательно, потенциальная энергия Е_П электрона внутри металла постоянна и ее можно выбрать за начало отсчета и считать равной 0.

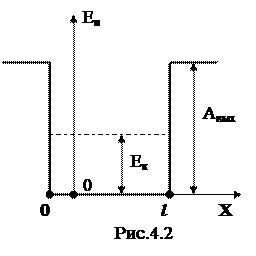На границах металла расположен двойной электрический слой, для преодоления которого нужно затратить работу выхода А_ВЫХ. Поэтому потенциальная энергия электрона вне металла Е_П= А_ВЫХ > 0.

Направим ось х перпендикулярно к грани бруска металла длиной l. Потенциальная энергия Е_п показана на рис.4.2.

Уравнение Шредингера в рассматриваемом случае имеет вид:

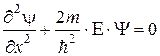, (т.к Е_п=0) (4.10)

Решением этого однородного дифференциального уравнения 2-го порядка является функция:

(4.11)

где k = 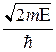, а С₁ и С₂ - постоянные, определяемые из граничных условий и условия нормировки.

Пока кинетическая энергия электрона мала по сравнению с высотой стенок «потенциальной ямы» электрон не имеет возможность выйти за пределы потенциальной ямы, поэтому граничные условия состоят в следующем:

(4.12)

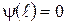(4.13)

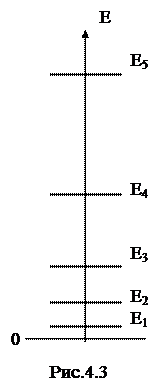Условие (4.12) после подстановки в (4.11) дает С₂ = 0, а условие (4.13) приводит к выражению sin k l = 0, из которого следует:

k l = nπ, где n =1, 2, 3… (4.14)

При этом учтено, что С₁ 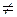0, т.к. электрон находится внутри ямы – это достоверно и что k 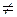0 в силу того, что электрон движется. Запишем выражение (4.14) в развернутом виде:

.

Откуда следует, что энергия электрона может иметь только дискретные значения Е_(n):

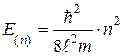(4.15)

На рис.4.3 дана схема разрешенных энергетических уравнений. Числа n называются «квантовыми» числами.

Заметим, что квантование энергии частиц впервые ввел Н.Бор ещё до создания квантовой механики.

Date: 2015-05-08; view: 730; Нарушение авторских прав