Волновая функция. Уравнение Шредингера

Невозможность одновременного точного нахождения координаты и импульса (координаты и скорости) частиц микромира заставило отказаться от классической механики в применении к рассматриваемому объекту, снять задачу о точном знании положения частиц и перейти к определению вероятности нахождения частицы в том или ином месте пространства. В результате была разработана специальная механика, изучающая поведение и состояния частиц микромира,- квантоваямеханика.

Одной из главных задач квантовой механики является нахождение волновой функции y = y(x,y,z,t). Произведение квадрата модуля волновой функции на элемент объема пространства |y|²×dV физически толкуется как вероятность того, что действие частицы будет обнаружено в элементе объема dV. Следовательно, |y|²× толкуется как плотность вероятности обнаружения частицы (электрона). Сумма величин |y|²×dV по всему пространству, т.е. 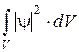есть вероятность обнаружения частицы где бы то ни было в пространстве. Но т.к. частица существует, следовательно, y -функция должна удовлетворять условию: 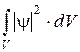=1 - УСЛОВИЕ НОРМИРОВКИ.

Если известна y -функция, описывающая состояние, то вероятности всевозможных процессов определяются однозначно.

Наличие волновых свойств у частиц микромира наводит на мысль о том, что к частицам должно быть применимо волновое уравнение, из которого как раз и может быть найдена волновая функция y:

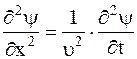(4.5)

где u - скорость распространения волны де Бройля. Удовлетворяющая этому дифференциальному уравнению функция y(x,t) имеет вид:

y(x,t) = y₀ × cos (ωt – kx) (4.6)

Беря вторую производную по времени от y -функции, заданной уравнением (4.6), получим:

(4.7)

Подставляя (4.7) в (4.5), находим: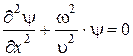

или поскольку ,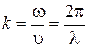

то 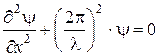(4.8)

В соответствии с гипотезой де Бройля заменим в выражении (4.8) величину l=h/P:

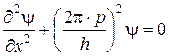(4.9)

Т.к.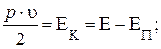

где Е и Е_П - соответственно полная и потенциальная энергия частицы, то

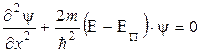
Это - СТАЦИОНАРНОЕ УРАВНЕНИЕ ШРЕДИНГЕРА.

4.5 Операторы физических величин. (Самостоятельно)

Различные виды волнового уравнения, рассмотренные выше, могут быть записаны в более удобной форме с помощью операторов. В общем случае: оператор – это некоторое правило, согласно которому, каждой функции, заданной в некоторой области, ставятся в соответствии новые функции, заданные в той же области.

Например: число 2, выступая в роли множителя, преобразует каждое значение функции, заданной на некотором промежутке, удваивая его. Причем область определения остается неизменной. В этом случае говорят, что 2 – есть арифметический оператор. Дифференциальный оператор 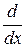, применяемый к функции 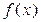в обычном смысле, преобразует каждое значение 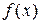в значение ее производной, т.е. .

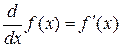Операторы только линейные (в квантовой механике). Это нужно, чтобы не нарушался принцип суперпозиций состояний.

Если , то .

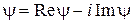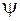и 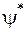- комплексно сопряженные величины.

Пример: волновая функция для свободной частицы 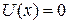(волны де Бройля).

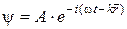
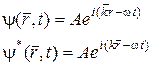- комплексные сопряженные функции.

Тогда среднее значение любой физической величины:

.

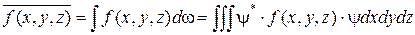Сама волновая пси-функция определяется из основного уравнения механики микрочастиц (квантовая механика – из уравнения Шредингера).

Если в механике (классической) основным был 2-ой закон Ньютона – опытный факт (постулат) в макромире. Он не выводится. Как и уравнение Шредингера, мы его получаем, опираясь на опытные факты: по дифракции микрочастиц. Из уравнения Шредингера, как частный случай уже можно вывести 2-ой закон Ньютона (теорема Эренфеста). Формально обосновать можно так: согласия с опытом можно достичь, если вместо физической величины (макро): 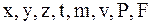и т.д. мы введем их микро аналоги – операторы (будем обозначать шляпками сверху).

Импульс:

.

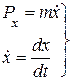
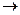
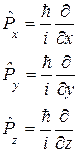Масса: .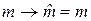

Энергия:

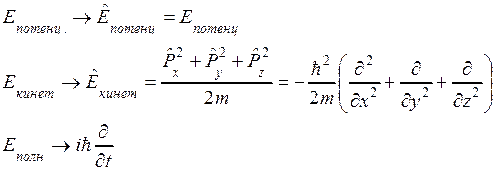
Если система консервативна, будет выполняться закон сохранения энергии механической, т.е. в операторной форме:

.

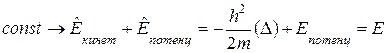Умножая на 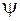, получим уравнение Шредингера:

.

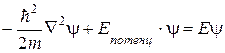Находим 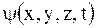. А затем все интересующие нас средние величины. Затем таким же образом находим собственные (дозволенные) значения интересующих нас величин. Исходим из граничных условий.

Электрон в «потенциальной яме»

Date: 2015-05-08; view: 698; Нарушение авторских прав