ВВЕДЕНИЕ. Как известно, для наблюдения интерференции света необходимо тем или иным способом создать когерентные волны

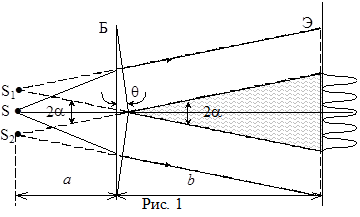Как известно, для наблюдения интерференции света необходимо тем или иным способом создать когерентные волны. В данной работе для получения когерентных волн используется бипризма Френеля. Она представляет собой симметричную призму с очень малым преломляющим углом q. Все лучи света, идущие через такую призму поворачивают на один и тот же малый угол a=(n-1)×q (n– показатель преломления бипризмы), отклоняясь в сторону вершины бипризмы (Рис. 1). Поэтому цилиндрическая волна, выходящая из освещенной щели S, параллельно ребру бипризмы, делится при­змой на две цилиндрических волны, как бы исходящих из мнимых когерентных источников S₁ и S₂. За призмой в области перекрытия световых волн (заштрихованная область) возникает интерференционная картина. Если щель освещается монохроматическим светом, то интерференционная картина наблюдается на экране Э и имеет вид чередующихся темных и светлых полос, параллельных ребру бипризмы.

Положение интерференционных полос и распределение интенсивности на экране изображено на Рис. 2, где d – расстояние между мнимыми источниками, которые при малых преломляющих углах бипризмы и малом угле падения лучей на бипризму находятся в одной плоскости со щелью; L – расстояние от плоскости 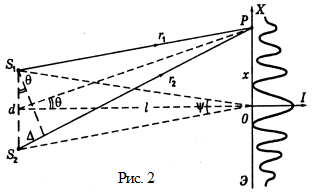источников до экрана Э.

Расстояние Dх между серединами соседних темных или светлых полос (между соседними максимумами или минимумами интенсивности) называется шириной интерференционной полосы[2]. Это расстояние нетрудно определить, воспользовавшись рисунком 2.

Определим координату полосы x. Из рисунка видно, что

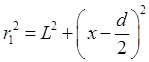и ,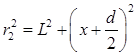

следовательно

.

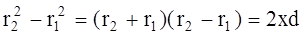Отсюда

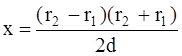(2).

Координаты светлых линий получим, если положим для них разность хода:

D=r₂–r₁=ml,

и соответственно, для темных линий:

D=ml+l/2.

Тогда ширину интерференционной полосы, т.е. расстояние между соседними темными или соседними светлыми полосами, получим как разность таких значений x, для которых значения m отличаются на единицу:

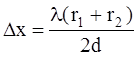(3).

Как видим, ширина интерференционной полосы Dx пропорциональна длине световой волны l. Поэтому для получения различимой интерференционной картины, т.е. достаточно больших Dx, нужны большие L и малые d. При таких условиях можно положить r₂ + r₁»2L, тогда ширина интерференционной полосы выразится соотношением:

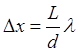(4).

Из формулы (4) получим длину световой волны:

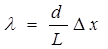(5)

Отметим здесь, что отношение d/L = y есть угол, под которым из центра интерференционной картины видны источники (щели), создающие интерференционную картину (см. Рис.2). Поэтому ширину интерференционной полосы можно записать так:

Dx = l/y.

Величины L и Dx, входящие в формулу (5) могут быть измерены непосредственно. Для определения d можно воспользоваться вспомогательной линзой Л и получить изображение d’ отрезка d. Измерив d’ и зная расстояние L от плоскости щели (плоскость отрезка d) до плоско­сти его изображения Э и расстояние a от плоскости щели до линзы, легко рассчитать d:

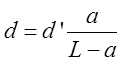(6).

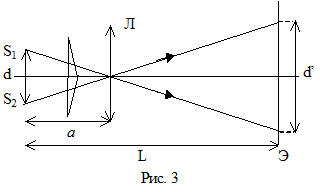Расстояние d может быть определено другим методом при условии, что L больше учетверенного фокусного расстояния линзы. В этом случае при двух положениях линзы Л₁ и Л₂ можно получить два изображения – увеличенное d’ и уменьшенное d”.

Из (6) получим, что 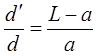. А второму положению линзы соответствует a’=L–a, что следует из формулы линзы. Тогда 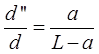, откуда расстояние d может быть вычислено по формуле:

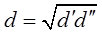(7).

Все рассуждения, на основе которых были получены (4) и (5) носили идеализированный, и поэтому весьма упрощенный характер. Реальная картина оказывается сложнее. Так свет, прошедший через светофильтр не является строго монохроматичным, длины световых волн принадлежат некоторому интервалу (l, l+Dl). Поскольку положение интерференционных полос на экране зависит от l, то картины, созданные волнами с различными l будут накладываться одна на другую, от чего результирующая картина будет размываться. Так, если на светлую полосу с некоторым номером N, созданную волной с длиной l накладывается темная полоса с номером (N-1) и длиной l+Dl, то в данном месте интерференционная картина исчезнет полностью. Таким образом, число полос N, которые мы увидим, определяется степенью монохроматичности l/Dl:

N=l/Dl.

Другой причиной, ухудшающей качество интерференционной картины, является конечный размер источника света (конечная ширина щели). Действительно, все рассуждения мы проводили для случая бесконечно узкой щели. Реально это не так, и разные участки щели создают на экране свои интерференционные картины, которые накладываются друг на друга. Ясно, что если в данной точке экрана свет от одного из участков щели дает темную полосу, а от другого светлую, то интерференционная картина исчезнет, экран окажется освещенным равномерно. Поэтому ширина щели должна быть достаточно малой.

Date: 2015-05-08; view: 803; Нарушение авторских прав