Главное в главе 1

Уравнение состояния идеального газа (часто называемое в России уравнением Менделеева–Клапейрона)

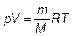(1.21)

хорошо известно из школьного курса физики.

Рассмотрены изотермический, изобарный, изохорный процессы в идеальном газе. Результаты приведены в табл. 6.1.

Изложена теория осмотического давления.

С использованием основных положений молекулярно-кинетической теории (МКТ):

1) вещество состоит из частиц;

2) эти частицы непрерывно и хаотически движутся;

3) частицы взаимодействуют между собой,

рассмотрены основы строения твердых, жидких и газообразных тел.

Для идеального газа на основе положений МКТ построено основное уравнение МКТ идеального газа:

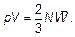(1.47)

Сравнение приведенных двух уравнений, описывающих один и тот же объект — идеальный газ, позволяет связать макроскопические характеристики газа с микроскопическими характеристиками отдельной молекулы. Средняя кинетическая энергия молекулы связывается с температурой газа

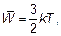(1.48)

где k = R / NА называется постоянной Больцмана.

Date: 2015-05-08; view: 730; Нарушение авторских прав