Молекулярные основы теории идеального газа

Так как расстояние между молекулами в газе в среднем гораздо (на порядок) больше, чем в жидкостях и твердых телах, то газы сжимаемы. Нужно в десятки раз уменьшить расстояние между молекулами, чтобы проявились силы отталкивания. Такому сближению соответствует уменьшение объема (пропорциональное третьей степени расстояния) во много тысяч раз.

Из-за больших расстояний можно слабыми силами отталкивания в газе вообще пренебречь, а из-за сильной сжимаемости считать, что силы отталкивания в газе проявляются только на расстояниях, сравнимых с размерами молекул (так оно, вообще говоря, и есть). Зато уж на расстояниях, равных удвоенному расстоянию между молекулами, силы отталкивания можно считать очень большими (бесконечно большими).

В результате потенциал взаимодействия молекул (см. рис. 1.10) в газе может быть сильно упрощен и заменен «бесконечной» ступенькой (рис. 1.12).

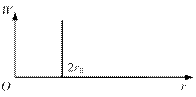
Рис. 1.12. Потенциал взаимодействия в идеальном газе

Конечно такой потенциал, он называется потенциалом твердых шаров, есть некоторое упрощение, идеализация реального потенциала. Оказалось, однако, что такая модель, в которой молекулы можно считать твердыми шариками, взаимодействующими только при сближении на расстояние, примерно равное (по порядку величины) радиусу этих шариков, очень продуктивно и хорошо (как и будет показано далее) описывает свойства газообразных сред.

Итак, идеальный газ — это ансамбль малых тел — «шариков», непрерывно и хаотически движущихся и взаимодействующих только при столкновении упругими силами.

Попытаемся теперь глубже понять, что такое беспорядочное, хаотическое движение, о котором говорится в основных положениях молекулярно-кинетической теории.

Рассмотрим среднюю, как говорится в математике, среднюю арифметическую скоростьмолекул газа. Среднее значение отмечается (обозначается) чертой сверху (без стрелки) или угловыми скобками. Оказывается, средняя арифметическая скорость молекул газа равна нулю (!).

(1.32)

В самом деле, для каждой скорости, например, 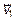всегда найдется равная ей по величине, но противоположно направленная скорость, например 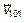. Их сумма равна нулю. Это проявление хаотичности, случайности скоростей движения молекул газа. Есть молекулы с любыми скоростями и направлениями.

Интересно и еще одно свойство больших ансамблей со случайными характеристиками (рис. 1.13). Одна какая-то наперед выбранная нами молекула, в течение длительного времени меняя свою скорость (например, из-за столкновений), обязательно будет иметь за это время все те значения и направления скорости, которые имеют молекулы «ансамбля» (рис. 1.13, а) в один (любой, но один) момент времени. (Сравните рис. 1.13, а и 1.13, б.) Это положение называется эргодической гипотезой. На самом деле это не гипотеза, а закон природы. Например, каждый человек за длительное время (за жизнь) проходит все возрасты. Если же набрать случайным образом большую группу людей, то среди них также будут люди всех возрастов. Этими «возрастами» члены группы обладают сейчас, в момент сбора группы. Примеры: жильцы дома, прохожие на улице. Студенты не образуют случайную совокупность по возрасту.

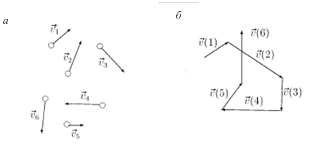
Рис. 1.13. Случайные скорости различных молекул в один и тот же момент времени (а). Случайные скорости одной молекулы в различные моменты времени (б). Скорости на рисунках справа и слева попарно равны

Рассмотрим теперь средний квадрат скорости молекул. Имеем

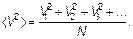(1.33)

Очевидно, 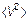средний квадрат скорости уже не равен нулю. Таким образом, наверное, характеристики движения молекул зависят от среднеквадратичной скорости (скалярной величины). От квадрата скорости зависит энергия (кинетическая энергия) молекулы. Средняя энергия и будет основной характеристикой молекулярного движения.

Date: 2015-05-08; view: 745; Нарушение авторских прав