Реальные газы

Окружающие нас и используемые в технологических процессах газы несколько отличаются от идеальных. Различие серьезно проявляется при давлениях в сотни атмосфер. При таких давлениях уже нельзя пренебрегать собственными объемами, занимаемыми молекулами, и их взаимодействием.

Обозначим собственный объем моля молекул данного газа b, тогда, очевидно, что в уравнении Менделеева–Клапейрона, нужно брать уже не общий объем V, а величину V — ν b, где ν — количество вещества. Такая запись показывает, что при V /ν >> b сжатие возможно свободно и газ близок по свойствам к идеальному. Если же 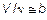, то сжимаемость ограничена и реальный газ больше напоминает несжимаемую жидкость.

Также теперь нельзя полностью пренебрегать притяжением между молекулами и заменять эмпирический потенциал взаимодействия (см., например, п. 1.5.3 и рис. 1.10 и 1.11) на потенциал взаимодействия твердых шаров (см. рис. 1.12). Уравнение состояния идеального газа при этом берется как первое приближение разложения давления р по плотности (p = ρ RT / M) или по обратным степеням объема одного моля газа ((V /ν)–1). К уравнению при этом добавляется слагаемое второго порядка, пропорциональное ρ2или (V /ν)–2. Сила взаимного притяжения молекул проявляется в дополнительном давлении а (V /ν)–2, где а — постоянная, зависящая от природы газа.

Оказывается, эти соображения позволяют найти формулу уравнения состояния, дающую правильные результаты в двух предельных случаях: идеальный газ и несжимаемая жидкость. Имеем:

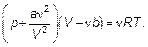(1.56)

Это уравнение Ван-дер-Ваальса.

Также как и для идеального газа (см. п. 1.8), зная уравнениесостояния (теперь это уравнение Ван-дер-Ваальса), можно записать выражение для внутренней энергии реального газа:

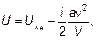(1.57)

где U ид = (i /2)ν RT — внутренняя энергия идеального газа(напоминаем, что i — число степеней свободы).

По уравнению состояния реального газа (формуле Ван-дер-Ваальса), можно найти:

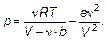(1.58)

Легко построить графики изотерм реального газа в осях p–V. Они представлены на рис. 1.20. Это кривые 1 – 1 ʹ, 2 – 2 ʹ,..., 6 – 6 ʹ. Изотермы проведены при температурах: T 1< T 2<... < T 6.

Рис. 1.20. Фазовая диаграмма перехода «жидкость—газ». Объяснения приведены в тексте

Вдали от изображенной пунктиром кривой AKB эти изотермы совпадают с опытными (экспериментальными) данными. Справа — хорошо известные изотермы идеального газа, проведенные в соответствии с законом Бойля–Мариотта, pV = const; слева — вертикальные линии, проведенные в соответствии с представлениями о несжимаемой жидкости, V = const. Вблизи от кривой AKB, и особенно внутри нее, изотермы, проведенные в соответствии с формулой (1.58), ничего общего с результатами экспериментов не имеют. Равновесный переход «газ—жидкость» происходит при постоянном давлении p = const. Соответствующие горизонтальные линии изображены на рис. 1.20 пунктиром. Таким образом, в осях p – V удобно изображать фазовый переход, например «газ—жидкость», и поэтому зависимость p–V называется фазовой диаграммой.

Интересно, что изотермы, построенные при температурах Т ≥ Т 4 = Т кр, показывают, что при температурах Т > Т крневозможно превратить газ в жидкость, невозможно сжижение газов. Сама точка K с характеристиками Т кр, V кр, р крсоответствует критическому состоянию вещества.

Величины T кр, V кри р крявляются характерными величинами температуры, объема и давления для данного газа. Введение безразмерных характеристик Т  ʹ = Т / Т кр, V ´= V / V кри р ʹ = р / р крпозволяет исключить характеристики вещества а, b и ν из уравнений и записать уравнение Ван-дер-Ваальса в виде:

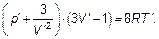(1.59)

Это уравнение состояния для всех тел, к которым вообще применимо уравнение Ван-дер-Ваальса. Состояния любых тел, в которых они имеют одинаковыми любую пару параметров Т  ʹ, V  ʹ, р ʹ, называются соответственными состояниями. Очевидно, что если два параметра в соответственных состояниях одинаковы, то третий параметр также будет одинаков при любом уравнении состояния. Это утверждение называется законом соответственных состояний.

Применение закона соответственных состояний позволяет переносить, моделировать, интерпретировать результаты действия лекарств, полученные при одних условиях, например на лабораторных животных, на другие условия, например на человека.

Date: 2015-05-08; view: 731; Нарушение авторских прав