Фазовые переходы

Переход вещества из одной фазы в другую называется фазовым переходом. Существуют два вида (или рода) фазовых переходов. Фазовые переходы первого рода сопровождаются выделением или поглощением теплоты, которую называют теплотой перехода. Удельной теплотой перехода 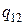называется количество теплоты, которое необходимо сообщить одному килограмму вещества, для того, чтобы при неизменных температуре и давлении перевести его из фазы 1 в фазу 2. Различают удельную теплоту парообразования (при переходе жидкость – газ и обратно), удельную теплоту плавления (переход кристалл – жидкость) и удельную теплоту сублимации (переход кристалл – газ).

Фазовые переходы второго рода происходят без поглощения или выделения теплоты. Ко второму роду относятся переходы проводник – сверхпроводник, парамагнетик – ферромагнетик и другие. В дальнейшем мы будем рассматривать только фазовые переходы первого рода.

Знакомство с фазовыми переходами начнем с перехода газ - жидкость, для чего проанализируем теоретические изотермы уравнения состояния реального газа Ван-дер-Ваальса (5.1) и сопоставим их с соответствующими экспериментальными кривыми. На рисунке 5.2 показаны три наиболее характерные изотермы уравнения Ван-дер-Ваальса при температурах 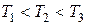. При достаточно высокой температуре Т ₃ изотерма уравнения Ван-дер-Ваальса близка к изотермам идеального газа (см. рис. 1.4). При некоторой температуре T ₂, называемой критической, на изотерме появляется точка перегиба К (критическая точка). При температуре 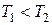на изотерме появляется волнообразный участок, причем на интервале АВ давление растет при увеличении объема, что, очевидно, в изотермическом процессе невозможно.

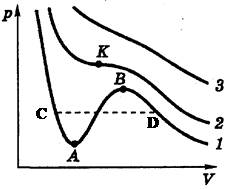
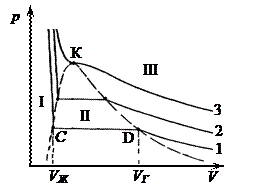
Рис. 5.2 Рис. 5.3

Экспериментальные зависимости давления реального газа от объема при постоянных температурах были впервые получены английским химиком Т. Эндрюсом[25] в 1866 г. Экспериментальные изотермы реального газа показаны на рисунке 5.3. Бросается в глаза, что, в отличие от теоретических, экспериментальные изотермы при температурах ниже критической имеют горизонтальный участок, на котором давление не зависит от объема. Рассмотрим это явление подробно.

Повторим мысленно опыт Эндрюса. Поместим газ в цилиндр, закрытый подвижным поршнем, и начнем сжимать его при постоянной температуре T ₁. Вплоть до объема V_Г, соответствующего точке D на рисунке 5.3, в цилиндре будет находиться только газ. При дальнейшем уменьшении объема в цилиндре помимо газа появится жидкость, количество которой будет расти, давление же в цилиндре будет оставаться постоянным (горизонтальный участок изотермы CD). При достижении объема V_Ж (точка С) цилиндр полностью будет заполнен жидкостью, газа не останется. Таким образом, на участке CD наблюдался фазовый переход газ – жидкость. Из описанного эксперимента следует, что, если фазовый переход совершается изотермически, то он происходит при постоянном давлении.

Горизонтальные участки присутствуют на всех изотермах при температурах ниже критической, но становятся все короче по мере увеличения температуры. Область II, ограниченная пунктиром на рисунке 5.3, соответствует двухфазной системе газ (пар) + жидкость, левее двухфазной области находится область температур и давлений I, где вещество может находиться только в жидком состоянии, а правее – область III, где вещество может быть только газообразным. Уравнение Ван-дер-Ваальса адекватно описывает состояние системы и в области III и в области I, т.е. может быть использовано в качестве уравнения состояния жидкости.

Состояния, соответствующие участкам СА и DB на теоретических изотермах уравнения Ван-дер-Ваальса (см. рис. 5.2), можно реализовать на практике, если вещество очистить от примесей и процесс проводить осторожно – медленно, не допуская механических сотрясений. Участок BD соответствует состоянию, называемому пересыщенным паром, а участок СА – состоянию перегретой жидкости. Эти состояния называются метастабильными. Они неравновесные, поскольку термодинамическому равновесию в данной области давлений и температур соответствует двухфазная система. Малейшее возмущение вещества, находящегося в метастабильном состоянии, приведет к переходу к равновесному двухфазному состоянию – перегретая жидкость закипит, а пересыщенный пар начнет конденсироваться.

Анализ изотерм уравнения Ван-дер-Ваальса показывает, что жидкая и газообразная фазы вещества при заданной температуре могут находится в равновесии (без переходов одной фазы в другую) лишь при одном строго определенном значении давления. Это утверждение является справедливым для всех без исключения двухфазных систем. Можно задать зависимость 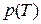, описывающую условия равновесия любой двухфазной системы. Такая зависимость может быть найдена из уравнения Клапейрона-Клаузиуса:

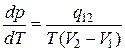, (5.4)

где 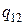- удельная теплота перехода, V ₁ и V ₂ – удельные объемы первой и второй фаз.

График рассчитанной при помощи уравнения (5.4) зависимости 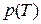, описывающий равновесие твердой и жидкой фаз, называют кривой плавления, жидкой и газообразной фаз – кривой испарения, твердой и газообразной фаз – кривой сублимации. Координатная плоскость, на которой показаны кривые плавления, испарения и сублимации какого-либо вещества, называется диаграммой состояний. Типичная диаграмма состояний изображена на рис. 5.4.

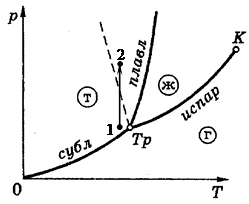
Рис. 5.4

Диаграмма состояний разделятся на три области, соответствующие твердой (Т), жидкой (Ж) и газообразной (Г) фазам. Равновесие между двумя фазами возможно только на их границе, между тремя – только в одной точке Тр, называемой тройственной точкой. Кривая испарения заканчивается критической точкой К, поскольку при температурах выше этой точки различия между жидкостью и паром исчезают.

Все без исключения процессы сублимации и парообразования проходят с увеличением удельного объема фазы (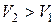), , 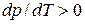поэтому кривые сублимации и испарения всегда описываются возрастающими функциями .

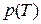При плавлении большинства веществ удельный объем также увеличивается, что и отражено на рис. 5.4. Однако, удельный объем некоторых веществ, в частности, воды, при плавлении уменьшается, а значит для них 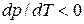. Соответствующая кривая плавления показана на диаграмме состояний пунктиром. Интересно отметить, что именно этой особенностью воды объясняется легкость, с которой скользят по льду стальные коньки. В обычном состоянии лед катка находится при температуре 260 – 270 К и нормальном атмосферном давлении (точка 1 на рис. 5.4). Лезвие конька имеет малую площадь и оказывает на лед большое давление, в результате чего мы переходим на диаграмме состояний из точки 1 в точку 2, соответствующую жидкой воде. Таким образом, вследствие сильного изотермического сжатия лед под коньком плавится, и образуется пленка воды, которая выполняет роль смазки, что сильно облегчает скольжение.

В заключение заметим, что равновесное состояние изолированной системы, состоящей более чем из трех фаз, невозможно.

Date: 2015-05-08; view: 2359; Нарушение авторских прав