Уравнение электронейтральности в неравновесных условиях

Как уже отмечалось в разделе 6, для получения в явном виде вольт-амперной характеристики транзистора необходимо найти связь между поверхностным потенциалом ψ _s и квазиуровнем Ферми φ _c. Рассмотрим для этого уравнение электронейтральности:

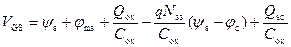. (6.59)

Заряд в ОПЗ состоит из заряда свободных электронов Q _n в канале и заряда ионизованных акцепторов Q _В, как показано в (6.54). Разложим заряд Q _В по степеням ψ _s вблизи порогового значения поверхностного потенциала ψ _s = 2 φ ₀.

Имеем:

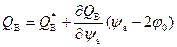, (6.60)

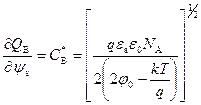. (6.61)

Величина C _B^* – емкость обедненной области при пороговом значении поверхностного потенциала ψ _s, 2 φ ₀.

С учетом (6.60) и (6.61) соотношение (6.59) примет вид:

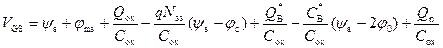. (6.62)

Назовем пороговым напряжением V _Т напряжение на затворе МДП‑транзистора V _GS в равновесных условиях (φ _c = 0), соответствующее пороговому потенциалу ψ _s = 2φ ₀:

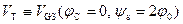. (6.63)

Из (6.62) и (6.63) следует, что

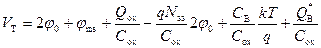. (6.64)

С учетом значений для порогового напряжения соотношения (6.64) уравнение электронейтральности примет вид:

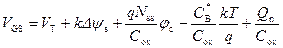, (6.65)

где n и Δ ψ _s будут равны:

.

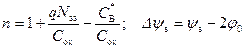Множитель n – число, характеризующее отношение емкости поверхностных состояний 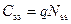и емкости обедненной области С _В к емкости подзатворного диэлектрика С _ox. Значения n могут лежать для реальных МДП‑структур в диапазоне 1÷5. Величина Δ ψ _s характеризует отклонение в данной точке поверхностного потенциала от порогового значения. Слагаемое 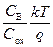в уравнении (6.65) соответствует заряду свободных электронов Q _n при пороговом значении поверхностного потенциала и обычно мало по сравнению с остальными слагаемыми, входящими в правую часть уравнения (6.65).

Для области слабой инверсии заряд свободных электронов мал и последним слагаемым в (6.65) можно пренебречь. Поскольку напряжение на затворе V _GS и пороговое напряжение V _Т – постоянные величины, то из (6.65) следует, что для области слабой инверсии в каждой точке инверсионного канала величина

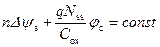
должна оставаться постоянной. Постоянную величину найдем из условия, что вблизи истока φ _c = 0 и, следовательно,

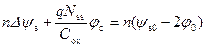. (6.66)

Отсюда следует, что в предпороговой области зависимость поверхностного потенциала ψ _s от квазиуровня Ферми φ _c будет определяться следующим выражением:

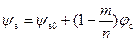, (6.67)

здесь ψ _s0 – значение поверхностного потенциала в точке канала, где φ _c = 0.

Величина m равна:

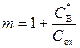. (6.68)

Таким образом, в МДП‑транзисторе в области слабой инверсии при отсутствии захвата на поверхностные состояния (N _ss = 0; m = n) поверхностный потенциал ψ _s не зависит от квазиуровня Ферми φ _c и, следовательно, постоянен вдоль инверсионного канала. Этот важный вывод обуславливает целый ряд особенностей в характеристиках МДП‑транзистора в области слабой инверсии.

Для области сильной инверсии при 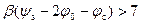в уравнении (6.65) в правой части доминирует слагаемое, связанное со свободными носителями заряда Q _W. Поэтому необходимо, чтобы вдоль канала в каждой точке величина заряда электронов Q _n оставалась постоянной. Поскольку в этой области для Q _n справедливо выражение (6.58), получаем:

.

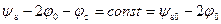Следовательно, в области сильной инверсии

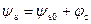. (6.69)

На рисунке 6.10 в качестве примера приведен расчет функциональной связи между ψ _s и φ _c по уравнению (6.65), выполненный численным методом. Параметры для расчета указаны в подписи к рисунку.

Рис. 6.10. Зависимость поверхностного потенциала ψ_s от величины квазиуровня Ферми φ _c в канале МОП ПТ при различных напряжениях затвора V _G, B.

V _T = 0,95 В; N _ss = 10¹² см^-2эВ^-1; N _A = 10¹⁶ см^-3; d _ox = 50 Å.

Пунктирная линия соответствует условию: ψ _s = 2φ ₀

Зная связь между поверхностным потенциалом ψ _s и величиной квазиуровня Ферми φ _c, можно получить соотношение между дрейфовой и диффузионной составляющими тока в произвольной точке канала. Действительно, из (6.46), (6.47) и (6.67) следует, что для области слабой инверсии

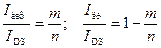. (6.70)

В области слабой инверсии при отсутствии захвата (N _ss = 0, m = n) весь ток канала диффузионный. При наличии захвата на поверхностные состояния появляется дрейфовая составляющая. Физически она обусловлена появлением продольного электрического поля за счет различия в заполнении поверхностных состояний вдоль канала. При заполнении поверхностных состояний основными носителями тока инверсионного канала дрейфовый и диффузионный ток имеют одно и то же направление. При условии постоянства плотности поверхностных состояний N _ss(ψ _s) в запрещенной зоне полупроводника соотношение между диффузионной и дрейфовой составляющей в области слабой инверсии сохраняется.

Для области сильной инверсии из (6.46), (6.47) и (6.69) следует, что диффузионный ток равен нулю и весь ток канала дрейфовый:

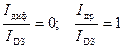. (6.71)

В области перехода от слабой к сильной инверсии доля дрейфовой составляющей в полном токе канала возрастает от значения, определяемого соотношением (6.70), до единицы.

6.11. Вольт-амперная характеристика МДП‑транзистора в области сильной и слабой инверсии

После того, как из решения уравнения Пуассона получена зависимость заряда свободных носителей Q _n(ψ _s, φ _c) как функция поверхностного потенциала и квазиуровня Ферми, а из уравнения непрерывности – связь между поверхностным потенциалом и квазиуровнем Ферми, можно вернуться к выражению для тока канала (6.43) и получить в явном виде вольт‑амперную характеристику МДП‑транзистора.

В области сильной инверсии из (6.43), (6.67) и (6.69) следует, что

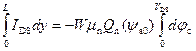. (6.72)

После интегрирования и учета того, что для области сильной инверсии в уравнении непрерывности (6.65) в правой части доминирует последний член, получаем:

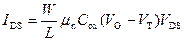. (6.73)

Отметим, что для области сильной инверсии, т.е. в приближении плавного канала, ВАХ МДП‑транзистора в виде (6.73) совпадает с ВАХ, полученной нами ранее в простейшем случае в виде (6.10).

В области слабой инверсии из (6.44), (6.57) и (6.67) следует, что

. (6.74)

После интегрирования (6.74) и учета того, что уравнение непрерывности (6.58) дает для этого случая

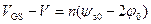, (6.75)

получаем:

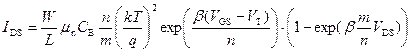. (6.76)

Соотношение (6.76) представляет собой вольт‑амперную характеристику МДП‑транзистора для области слабой инверсии. На рисунках 6.11, 6.12 приведены проходные и переходные характеристики транзистора в этой области. Обращает на себя внимание тот факт, что в области слабой инверсии зависимость тока стока I _DS от напряжения на затворе V _GS – экспоненциальная функция, причем экспоненциальный закон сохраняется на много порядков. Ток стока не зависит практически от напряжения на стоке, выходя на насыщение при напряжениях исток-сток V _DS порядка долей вольта. Напомним, что при слабом захвате (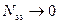) ток канала имеет диффузионный характер. Для случая, когда МДП-транзистор работает при напряжениях на затворе V _GS больше порогового напряжения V _T и напряжениях на стоке V _DS больше напряжения отсечки V _DS^*, т.е. в области насыщения тока стока, ситуация усложняется. Точка отсечки соответствует переходу от области сильной к области слабой инверсии. Слева к истоку от точки отсечки канал находится в области сильной инверсии, ток в канале дрейфовый, заряд свободных электронов постоянен вдоль канала. Справа к стоку от точки отсечки область канала находится в слабой инверсии, ток в канале диффузионный, заряд свободных электронов линейно изменяется вдоль инверсионного канала. На рисунке 6.10 видно, что область перехода от сильной к слабой инверсии на зависимости ψ _s = φ _c выражается перегибом, что соответствует изменению соотношения между дрейфовой и диффузионными составляющими тока канала. Таким образом, в области отсечки ток в канале вблизи истока в основном дрейфовый, при приближении к стоку в области отсечки резко возрастет диффузионная составляющая, которая при нулевом захвате равна у стока полному току канала.

Предыдущий анализ позволяет получить распределение вдоль инверсионного канала квазиуровня Ферми φ _c, его градиента 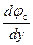и заряда свободных носителей Q _n(у). За основу возьмем выражение для полного тока в канале в виде (6.44). Будем считать, что подвижность μ _n не меняется вдоль инверсионного канала. Из условия непрерывности тока следует, что произведение

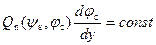(6.77)

должно оставаться величиной, постоянной вдоль инверсионного канала. Заметим, что при больших величинах напряжения исток-сток V _DS допущение о постоянстве подвижности μ _n = const может не выполняться. Физически зависимость подвижности μ _n от положения вдоль канала может быть обусловлена

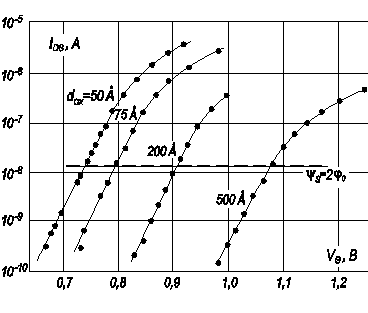
Рис. 6.11. Зависимость тока стока I _DS от напряжения на затворе V _G в предпороговой области для МДП‑транзисторов с разной толщиной подзатворного диэлектрика. Стрелками на кривых показаны области перехода от экспоненциальной к более плавной зависимости тока стока I _DS от напряжения на затворе. Напряжение исток-сток V _DS = 0,025 В

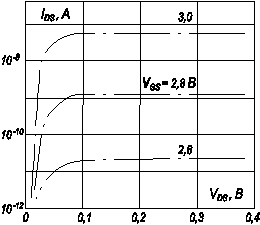
Рис. 6.12. Зависимость тока стока I _DS от напряжения на стоке V _DS в области слабой инверсии при различных предпороговых значениях напряжения на затворе V _G. V _T = 2,95 В

ее зависимостью от концентрации свободных носителей. Поэтому в дальнейшем будем считать напряжение исток-сток V _DS малым, когда μ _n = const.

Для области слабой и сильной инверсий соотношения (6.57), (6.67), (6.58), (6.69) дают соответственно:

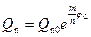; (6.78)

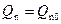, (6.79)

где Q _n0 – заряд электронов в канале при φ _c = 0 (или вблизи истока, или при равновесных условиях).

Проведем интегрирование уравнения (6.77) с учетом (6.78) и (6.79) и с граничными условиями:

.

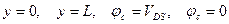Предполагается, что длина канала L много больше области изменения легирующей концентрации вблизи стока и истока.

Получаем выражения для распределения квазиуровня Ферми вдоль канала в области слабой инверсии:

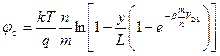. (6.80)

Для градиента квазиуровня получаем после дифференцирования (6.80):

. (6.81)

Поскольку вдоль инверсионного канала произведение (6.77) остается постоянным, то, следовательно, заряд свободных электронов Q _n линейно спадает вдоль канала, как вытекает из (6.81):

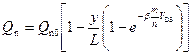. (6.82)

Ha рисунке 6.13а, б приведены величины квазиуровня и его градиента 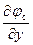как функция координаты вдоль канала у в области слабой инверсии.

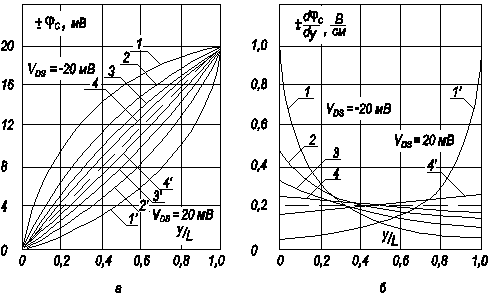
Рис. 6.13. Распределение потенциала вдоль инверсионного канала

а) распределение квазиуровня Ферми φ _c; б) распределение градиента квазиуровня Ферми 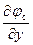вдоль инверсионного канала: 1,1’ – m/n =1; 2,2’ – m/n = 0,5; T = 80 K, 3,3’ – m/n = 1; 4,4’ – m/n = 0,5; T = 290 K.

Пунктирная линия соответствует линейному распределению квазиуровня Ферми φ _c вдоль канала

Для области сильной инверсии (6.77) с учетом (6.79) и (6.80) дает:

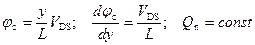. (6.83)

Следовательно, в области сильной инверсии квазиуровень Ферми φ _c линейно меняется вдоль канала, заряд электронов постоянен в каждой точке канала. Отметим, что соотношения (6.58), (6.69), являющиеся основой (6.79), справедливы в области сильной инверсии, когда 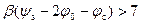. Численный расчет уравнения (6.77) для всего реально изменяющегося диапазона поверхностных избытков Г _n приведен на рисунке 6.14. Из рисунка 6.14 следует, что в области избытков Г_n << 10⁹ см^-2 справедливы соотношения (6.80 – 6.82), а в области Г _n > 10¹² см^-2 – соотношения (6.83). В промежуточной области необходим численный расчет.

Рис. 6.14. Зависимость квазиуровня Ферми φ_c в точке канала y/L = 0,3 в зависимости от избытка электронов Г _n при равных температурах Т и напряжениях V _DS. Точки – эксперимент, сплошная линия – расчет

6.12. МДП‑транзистор как элемент памяти

Рассмотрим RC ‑цепочку, состоящую из последовательно соединенных нагрузочного сопротивления R _H ≈ 1 МОм и полевого транзистора с изолированным затвором, приведенную на рисунке 6.15а, б. Если в такой схеме МДП-транзистор открыт, сопротивление его канала составляет десятки или сотни Oм, все напряжение питания падает на нагрузочном сопротивлении R _Н и выходное напряжение U _вых близко к нулю.

Если МДП-транзистор при таком соединении закрыт, сопротивление между областями истока и стока велико (сопротивление р‑n перехода при обратном включении), все напряжение питания падает на транзисторе и выходное напряжение U _вых близко к напряжению питания U _пит. Как видно из приведенного примера, на основе системы резистор – МДП-транзистор легко реализуется элементарная логическая ячейка с двумя значениями: ноль и единица. Реализовать такую схему можно несколькими вариантами. В одном из них выбирается МДП‑транзистор со встроенным каналом и при напряжении на затворе, равном нулю, реализуется случай, соответствующий приведенному на рисунке 6.15а.

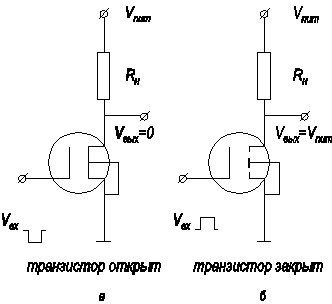
Рис. 6.15. Схема, поясняющая работу МДП‑транзистора в качестве элемента запоминающего устройства

а) открытое состояние; б) закрытое состояние

После подачи на затвор напряжения V _G транзистор закрывается и реализуется условие, показанное на рисунке 6.15б. В другом варианте выбирается МДП‑транзистор с индуцированным каналом и при напряжении на затворе V _G, равном нулю, транзистор закрыт и реализуется случай, приведенный на рисунке 6.15б. При подаче на затвор обедняющего напряжения транзистор открывается и реализуется случай, соответствующий приведенному на рисунке 6.15а.

Одним из недостатков приведенной элементарной ячейки информации является необходимость подведения на все время хранения информации напряжения к затворному электроду. При отключении напряжения питания записанная информация теряется. Этого недостатка можно было бы избежать, если в качестве МДП-транзистора использовать такой транзистор, у которого регулируемым образом можно было бы менять пороговое напряжение V _T. Тогда при положительном пороговом напряжении V _T > 0 (n -канальный транзистор) МДП‑транзистор закрыт и реализуется случай, соответствующий приведенному на рисунке 6.18б. При отрицательном пороговом напряжении V _T < 0 МДП‑транзистор закрыт и реализуется случай, соответствующий приведенному на рисунке 6.18а.

6.13. МНОП‑транзистор

Величина порогового напряжения V _T определяется уравнением (6.64). Как видно из этого уравнения, для изменения величины порогового напряжения V _T необходимо:

а) изменить легирование подложки N _A (для изменения объемного положения уровня Ферми φ ₀, разности paбот выхода φ _ms, заряда акцепторов в области обеднения Q _В);

б) изменить плотность поверхностных состояний N _ss;

в) изменить встроенный в диэлектрик заряд Q _ох;

г) изменить напряжение смещения канал‑подложка V _SS (для изменения заряда акцепторов Q _В в слое обеднения). Поскольку информацию в ячейку необходимо перезаписывать многократно, случаи а) и б) для этого оказываются непригодными. Случай г) не подходит вследствие того, что при отключении напряжения информация не сохраняется. Таким образом, для реализации энергонезависимого репрограммируемого полупроводникового запоминающего устройства (РПЗУ) необходим МДП‑транзистор, в котором обратимым образом было бы возможно изменять пороговое напряжение V _T за счет изменения встроенного в диэлектрик заряда Q _ох.

Наиболее распространенными РПЗУ, в которых реализован этот принцип, являются РПЗУ на основе полевых транзисторов со структурой металл – нитрид – окисел – полупроводник (МНОП‑транзисторы) и на основе полевых транзисторов с плавающим затвором.

На рисунке 6.16а, б приведена схема, показывающая основные конструктивные элементы МНОП ПТ и МОП ПТ с плавающим затвором.

В МНОП ПТ в качестве подзатворного диэлектрика используется двухслойное покрытие. В качестве первого диэлектрика используется туннельно прозрачный слой (d _ox < 50 Å) двуокиси кремния. В качестве второго диэлектрика исполь­зуется толстый (d ≈ 1000 Å) слой нитрида кремния. Нитрид кремния Si₃N₄ имеет глубокие ловушки в запрещенной зоне и значение диэлектрической постоянной 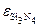в два раза более высокое, чем диэлектрическая постоянная двуокиси кремния SiO₂. Ширина запрещенной зоны нитрида Si₃N₄ меньше, чем ширина запрещенной зоны окисла SiO₂.

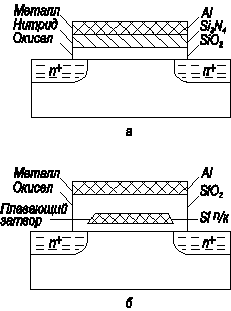
Рис. 6.16. Топология полупроводниковых запоминающих устройств:

а) МНОП‑транзистор; б) МОП ПТ с плавающим затвором

На рисунке 6.17а приведена зонная диаграмма МНОП‑транзистора. Рассмотрим основные физические процессы, протекающие в МНОП‑транзисторе при работе в режиме запоминающего устройства. При подаче импульса положительного напряжения + V _GS на затвор вследствие разницы в величинах диэлектрических постоянных окисла и нитрида в окисле возникает сильное электрическое поле. Это поле вызывает, как показано на рисунке 6.17б, туннельную инжекцию электронов из полупроводника через окисел в нитрид. Инжектированные электроны захватываются на глубине уровня ловушек в запрещенной зоне нитрида кремния, обуславливая отрицательный по знаку встроенный в диэлектрик заряд. После снятия напряжения с затвора инжектированный заряд длительное время хранится на ловушечных центрах, что соответствует существованию встроенного инверсионного канала. При подаче импульса отрицательного напряжения - V _GS на затвор происходит туннелирование электронов с ловушек в нитриде кремния в зону проводимости полупроводника, как показано на рисунке 6.17в. При снятии напряжения с затвора зонная диаграмма МНОП‑структуры снова имеет вид, как на рисунке 6.17а, и инверсионный канал исчезает.

Оценим величину инжектированного заряда, необходимую для переключения МНОП‑транзистора. Пусть величина Δ V _T = 10 В, , .

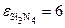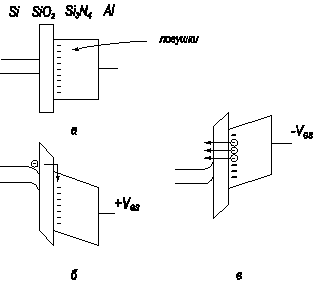
Рис. 6.17. Зонная диаграмма МНОП‑транзистора:

а) напряжение на затворе равно нулю, ловушки не заполнены; б) запись информационного заряда; в) стирание информационного заряда

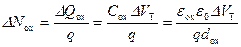. (6.84)

Подставив численные значения в (6.84), получаем Δ N _ox ≈ 3·10¹¹ см^-2. Считая, что захват идет в энергетический интервал 1 эВ в запрещенной зоне нитрида и в слой толщиной 100 Å, получаем, что энергетическая плотность объемных ловушек N _t в нитриде должна быть порядка 2·10¹⁸ см^-3·эВ^-1.

Date: 2015-05-05; view: 862; Нарушение авторских прав