Методы определения параметров МОП ПТ из характеристик

Покажем, как можно из характеристик транзистора определять параметры полупроводниковой подложки, диэлектрика и самого транзистора. Длину канала L и ширину W обычно знают из топологии транзистора. Удельную емкость подзатворного диэлектрика С _ox, а следовательно, и его толщину находят из измерения емкости C‑V затвора в обогащении. Величину порогового напряжения V _T и подвижность μ _n можно рассчитать как из характеристик в области плавного канала (6.10), так и из характеристик транзистора в области отсечки (6.12). В области плавного качала зависимость тока стока I _DS от напряжения на затворе V _GS – прямая линия. Экстраполяция прямолинейного участка зависимости I _DS(V _GS) к значению I _DS = 0 соответствует, согласно (6.10),

. (6.32)

Тангенс угла наклона tg (α) зависимости I _DS(V _GS) определяет величину подвижности μ _n:

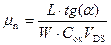. (6.33)

В области отсечки зависимость корня квадратного из тока стока I _DS от напряжения на затворе V _GS также, согласно (6.12), должна быть линейной. Экстраполяция этой зависимости к нулевому току дает пороговое напряжение V _T.

Тангенс угла наклона tg (α) зависимости определит величину подвижности μ _n:

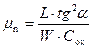. (6.34)

На рисунке 6.5 были приведены соответствующие зависимости и указаны точки экстраполяции. Для определения величины и профиля легирования N _A(z) пользуются зависимостью порогового напряжения V _T от смещения канал-подложка V _SS. Действительно, как следует из (6.18), тангенс угла наклона tg (α) зависимости 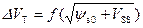определяет концентрацию легирующей примеси. Зная толщину окисла и примерное значение N _A (с точностью до порядка для определения 2 φ ₀), из (6.18) можно рассчитать величину и профиль распределения легирующей примеси в подложке МДП‑транзистора:

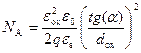. (6.35)

Эффективная глубина z, соответствующая данному легированию, равна:

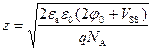. (6.36)

Таким образом, из характеристик МДП‑транзистора можно рассчитать большое количество параметров, характеризующих полупроводник, диэлектрик и границу раздела между ними.

6.7. Подпороговые характеристики МДП‑транзистора

При анализе характеристик полевых МДП‑транзисторов в дрейфовом приближении, проведенном выше, не учитывалась диффузионная компонента тока. В связи с этим, из соотношения (6.9) следовало, что при напряжении на затворе ниже порогового напряжения, заряд неравновесных носителей в инверсионном канале Q _n был равен нулю и соответственно, ток между стоком и истоком отсутствовал. В то же время известно, что для области слабой инверсии (V _G < V _T, y _s < 2 j ₀), заряд неравновесных носителей хотя и мал, но отличен от нуля. Следовательно, будет отличен от нуля и ток между истоком и стоком. Область характеристик полевого транзистора при напряжении на затворе меньше порогового напряжения получила название подпороговых характеристик. Для анализа подпороговых характеристик необходимо рассмотреть параметры области пространственного заряда полупроводника в неравновесных условиях с учетом дрейфовой и диффузионной компонент тока.

Рассмотрим область пространственного заряда (ОПЗ) полупроводника в неравновесных условиях, когда приложено напряжение между областями истока и стока и течет электрический ток. Исток будем считать соединенным с подложкой. В этом случае между каждой точкой инверсионного канала и квазинейтральным объемом, так же как для случая смещенного р‑n перехода, будет расщепление квазиуровней Ферми для электронов F _n и дырок F _p, причем величина этого расщепления F _n – F _p = q·V (y) зависит от координаты у вдоль инверсионного канала. Поскольку в квазинейтральном объеме квазиуровни Ферми для электронов и дырок совпадают, то величина отщепления квазиуровня Ферми электронов F _n на поверхности полупроводника по отношению к уровню Ферми в нейтральном объеме будет равна φ _c = V (y).

На рисунке 6.9а, б приведены зонные диаграммы ОПЗ полупроводника соответственно в равновесных и неравновесных условиях, где указаны величины поверхностного потенциала ψ _s и квазиуровня Ферми φ _c.

Рис. 6.9. Зонная диаграмма поверхности полупроводника р ‑типа:

а) при равновесных условиях; б) при неравновесных условиях

Будем рассматривать полупроводник р ‑типа. Как следует из статистики заполнения электронами и дырками разрешенных зон, концентрация свободных носителей определяется расстоянием от квазиуровня Ферми до середины запрещенной зоны.

Имеем, как видно из зонных диаграмм,

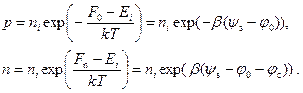(6.37)

Легко проверить, что в (6.37) выполняется фундаментальное coотношение, касающееся произведения концентраций неравновесных носителей:

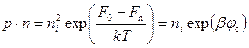. (6.38)

Date: 2015-05-05; view: 668; Нарушение авторских прав