Учет диффузионного тока в канале

Запишем выражение для плотности тока в канале МДП‑транзистора с учетом дрейфовой и диффузионной составляющих тока. Имеем:

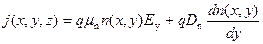. (6.39)

Величина тангенциальной составляющей электрического поля Е _y, согласно определению, равна:

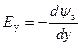. (6.40)

Градиент концентрации электронов 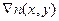вдоль инверсионного канала обусловлен наличием разности потенциалов между областями истока и стока и, как следует из соотношения (6.37), определяется градиентом квазиуровня Ферми φ _c. Из (6.37) имеем:

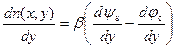. (6.41)

Воспользуемся соотношением Эйнштейна, связывающим подвижность электронов μ _n и коэффициент диффузии D _n.

.

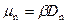Подставим соотношения (6.40 – 6.41) в выражение для плотности тока (6.39). Получаем:

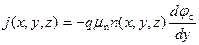. (6.42)

Проведя интегрирование по глубине z и ширине х инверсионного канала транзистора аналогично рассмотренному в главе 6, приходим к выражению для тока канала I _DS в виде:

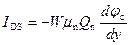. (6.43)

Как следует из соотношения (6.43), полный ток канала I _DS обусловлен градиентом квазиуровня Ферми вдоль инверсионного канала. Дрейфовая составляющая тока I _др будет равна:

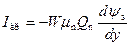. (6.44)

Диффузионная составляющая тока I _диф будет равна:

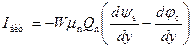. (6.45)

Если теперь из (6.43 – 6.45) выразим доли дрейфовой и диффузионной составляющих тока в полном токе канала МДП‑транзистора, то получим соответственно:

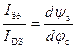; (6.46)

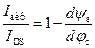. (6.47)

Таким образом, чтобы получить выражение для вольт-амперной характеристики МДП-транзистора с учетом дрейфовой и диффузионной составляющих, необходимо:

а) найти для соотношения (6.43) зависимость заряда неравновесных электронов Q _n как функцию поверхностного потенциала ψ _s и квазиуровня Ферми φ _c, т.е. Q _n(ψ _s, φ _c);

б) найти связь между поверхностным потенциалом и квазиуровнем Ферми ψ _s = ψ _s(φ _c);

в) найти зависимость поверхностного потенциала ψ _s от напряжений на затворе V _GS и стоке V _DS.

Date: 2015-05-05; view: 509; Нарушение авторских прав