
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Прямая, заданная пересечением двух плоскостей
|
|
Если плоскости 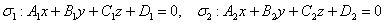 пересекаются,
пересекаются,
то система линейных уравнений 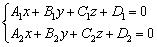 задаёт прямую в пространстве.
задаёт прямую в пространстве.
То есть прямая задана уравнениями двух плоскостей. Типовая и распространенная задача состоит в том, чтобы переписать уравнения прямой в каноническом виде:
Пример 9
Записать канонические уравнения прямой 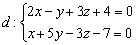
Решение: Чтобы составить канонические уравнения прямой, необходимо знать точку и направляющий вектор. А у нас даны уравнения двух плоскостей….
1) Сначала найдём какую-либо точку, принадлежащую данной прямой. Как это сделать? В системе уравнений нужно обнулить какую-нибудь координату. Пусть  , тогда получаем систему двух линейных уравнений с двумя неизвестными:
, тогда получаем систему двух линейных уравнений с двумя неизвестными: 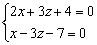 . Почленно складываем уравнения и находим решение системы:
. Почленно складываем уравнения и находим решение системы:
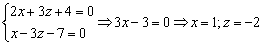
Таким образом, точка  принадлежит данной прямой. Обратите внимание на следующий технический момент: желательно найти точку с целыми координатами. Если бы в системе мы обнулили «икс» или «зет», то не факт, что получилась бы «хорошая» точка без дробных координат. Такой анализ и подбор точки следует проводить мысленно или на черновике.
принадлежит данной прямой. Обратите внимание на следующий технический момент: желательно найти точку с целыми координатами. Если бы в системе мы обнулили «икс» или «зет», то не факт, что получилась бы «хорошая» точка без дробных координат. Такой анализ и подбор точки следует проводить мысленно или на черновике.
Выполним проверку: подставим координаты точки  в исходную систему уравнений:
в исходную систему уравнений: 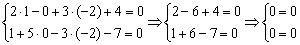 . Получены верные равенства, значит, действительно
. Получены верные равенства, значит, действительно 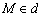 .
.
2) Как найти направляющий вектор прямой? Его нахождение наглядно демонстрирует следующий схематический чертёж:
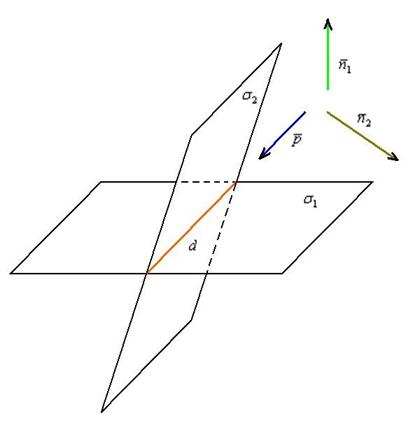
Направляющий вектор нашей прямой ортогонален нормальным векторам плоскостей. А если 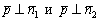 , то вектор «пэ» найдём как векторное произведение векторов нормали:
, то вектор «пэ» найдём как векторное произведение векторов нормали:  .
.
Из уравнений плоскостей 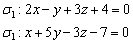 снимаем их векторы нормали:
снимаем их векторы нормали:
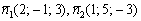
И находим направляющий вектор прямой:
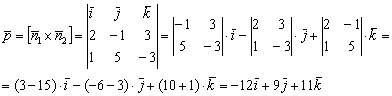
Как проверить результат, рассматривалось в статье Векторное произведение векторов.
3) Составим канонические уравнения прямой по точке  и направляющему вектору
и направляющему вектору 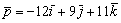 :
:
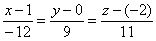
Ответ: 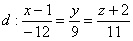
На практике можно пользоваться готовой формулой: если прямая задана пересечением двух плоскостей 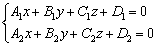 , то вектор
, то вектор 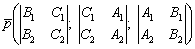 является направляющим вектором данной прямой.
является направляющим вектором данной прямой.
Пример 10
Записать канонические уравнения прямой 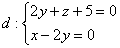
Это пример для самостоятельного решения. Ваш ответ может отличаться от моего ответа (смотря, какую точку подберёте). Если отличие есть, то для проверки возьмите точку из вашего уравнения и подставьте в моё уравнение (или наоборот).
Полное решение и ответ в конце урока.
Во второй части урока мы рассмотрим взаимное расположению прямых в пространстве, а также разберём задачи, которые связаны с пространственными прямыми и точками. Терзают меня смутные ожидания, что материала будет прилично, поэтому лучше всё-таки сделать отдельную веб страницу.
Добро пожаловать: Задачи с прямой в пространстве >>>
Решения и ответы:
Пример 4: Ответы:
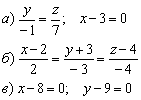
Пример 6: Решение: Найдём направляющий вектор прямой:
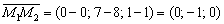
Уравнения прямой составим по точке 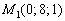 и направляющему вектору
и направляющему вектору 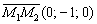 :
:
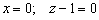
Ответ: 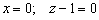 («игрек» – любое)
(«игрек» – любое)
Пример 8: Решения и ответы:
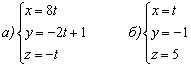
в) Найдём направляющий вектор прямой: 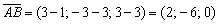 . Параметрические уравнения прямой составим по точке
. Параметрические уравнения прямой составим по точке 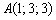 (можно выбрать точку «бэ») и направляющему вектору
(можно выбрать точку «бэ») и направляющему вектору  :
:
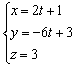
Пример 10: Решение: Найдём какую-нибудь точку, принадлежащую данной прямой. Пусть  , тогда:
, тогда: 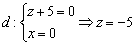 . Точка
. Точка 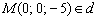 . Найдём направляющий вектор прямой, используем формулу:
. Найдём направляющий вектор прямой, используем формулу:

Составим канонические уравнения прямой по точке 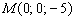 и направляющему вектору
и направляющему вектору  :
:
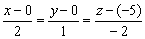
Ответ: 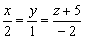
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)
Как можно отблагодарить автора?
Date: 2015-04-23; view: 1071; Нарушение авторских прав