Директрисы эллипса

Директриса, как вы помните из материалов о параболе, – это прямая. Причём прямая с армией горячих поклонников. Сейчас изучал статистику запросов Яндекса – за месяц около 1000 человек искали поpnо с директрисой и примерно 600-т любителей геометрии изъявили желание её тpа)(нyть =) Ну что же, шалуны, завидуйте, у эллипса две директрисы!

Канонически расположенный эллипс 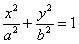имеет две директрисы, которые задаются уравнениями 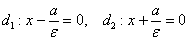, где «эпсилон» – эксцентриситет данного эллипса.

Для нашего героя :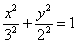

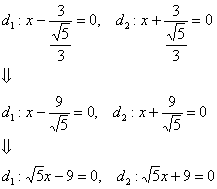
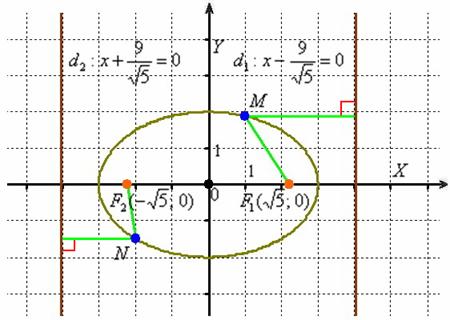
Так и есть, первая директриса полностью совпала с прямой «дэ». Более того, в условии задачи фактически сформулирована следующая теорема аналитической геометрии:

Эллипс – есть множество всех точек плоскости, таких, что отношение расстояния до каждой точки от фокуса к расстоянию от неё до соответствующей (ближайшей) директрисы равно эксцентриситету:

То есть, для любой точки 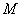эллипса отношение её расстояния от фокуса 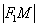к расстоянию от неё же до ближайшей директрисы 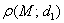в точности равно эксцентриситету: .

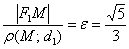Со вторым фокусом и второй директрисой аналогичная история, какую бы точку 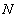эллипса мы ни взяли – будет справедливо отношение: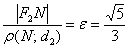

Ответ: искомое геометрическое место точек представляет собой эллипс 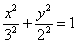с фокусами 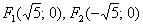и эксцентриситетом 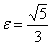. Уравнения директрис: .

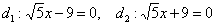Похожий пример для самостоятельного решения:

Задача 6

Найти уравнение геометрического места точек, для каждой из которых отношение расстояния до точки 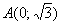к расстоянию до прямой 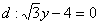постоянно и равно 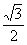. Выполнить чертеж. Привести уравнение линии к каноническому виду, найти фокусы, эксцентриситет, асимптоты и директрисы, если они существуют.

В образце решения концовка реализована обоими способами, выбирайте версию, которая более уместна в вашем курсе высшей математики.

Наша вечеринка в самом разгаре, и вокруг происходит столько интересного, что, порой, и говорить об этом неловко =) Зажигаем дальше!

Задача 7

Составить уравнение линии, для каждой из которых разность расстояний до точек 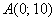и 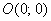по модулю равна 8. Привести уравнение к каноническому виду и выполнить чертёж. Найти асимптоты, фокусы, эксцентриситет и директрисы, если они существуют.

Решение: пусть точка 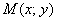принадлежит искомой линии. Тогда:

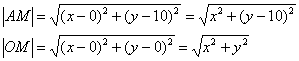
По условию:

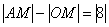
Или:

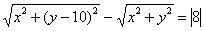
Кстати, ничего не напоминает? Внимательные читатели уже определили линию;-)

Корни? Модуль? Застрелитесь! Ерунда!

Сначала нужно избавиться от радикалов. Поскольку возводить в квадрат сразу – идея плохая (экспериментаторы могут попробовать), разведём корни по углам ринга:

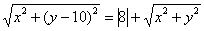
Ну вот, теперь совсем другое дело:

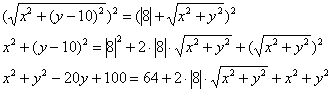
Успехи есть, но один корень остался. Оставим нашего зловреда в одиночестве и максимально упростим левую часть уравнения:

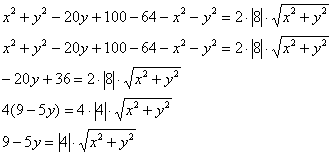
Возводим в квадрат обе части ещё раз, заметьте, как попутно и совершенно спокойно завершается расправа с модулем:

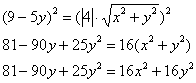
Перебросим всё направо и «развернём» уравнение:

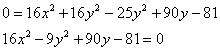
Получено уравнение линии 2-го порядка в общем виде. Выделяем полный квадрат при переменной «игрек», для этого вынесем «минус девять» за скобку:

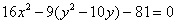
Далее внутри искусственно добавляем +25 (в целях применения формулы 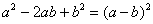на следующем шаге) и, чтобы всё выражение не изменилось, за скобками нужно прибавить :

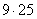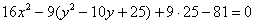
Хорошо осмыслите выполненное действие – фишка распространённая.

Собираем квадрат разности и допиливаем константы:

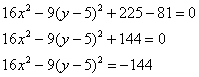
Вот тебе и раз. По всем признакам мыльная опера должна была закончиться гиперболой 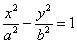, но у нас «лишний» минус. Выполним проверку и раскроем скобки (что желательно сделать в любом случае)… нет, всё верно – получается исходное общее уравнение .

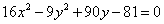Изменим знаки у обеих частей:

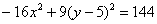
Уже ближе к правде, но «минус» оказался «не на своём месте». В главе о повороте и параллельном переносе гиперболы я рассказывал, что это признак поворота данной кривой на 90 градусов относительно своего канонического положения.

Но давайте сначала доведём до ума уравнение. Делим обе части на 144:

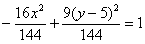
И завершающий тонкий тюнинг:

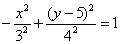– вот она, долгожданная гипербола, удовлетворяющая условию задачи,...которое фактически представляет собой определение гиперболы =)

По условию требуется сначала привести уравнение к каноническому виду, и только потом выполнить чертёж. Дабы не превысить точку кипения серого вещества, применим упрощенную схему. Однако случай всё равно не самый простой. Центр симметрии нашей подопечной находится в точке 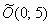, и, кроме того, она повёрнута на 90 градусов вокруг этой точки

На первом шаге осуществим параллельный перенос гиперболы 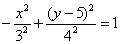ТАК – чтобы её центр оказался в начале координат. В результате получится уравнение: .

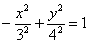Вторым действием повернём гиперболу вокруг начала координат на 90 градусов, при этом меняем местами значения полуосей и перебрасываем «минус» к переменной «игрек»:

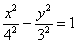
В принципе, операции перестановочны, т.е. сначала можно было повернуть вокруг точки 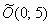, а потом перенести центр в начало координат.

Не забывая про асимптоты 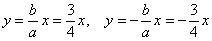, выполним чертёж:

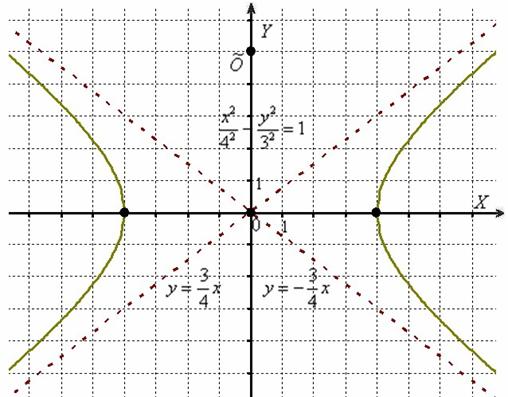
Еще раз: как расположена исходная гипербола 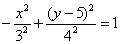? Она получена поворотом канонической гиперболы 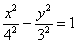на 90 градусов вокруг начала координат и дальнейшим переносом вдоль оси 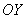на 5 единиц вверх центром симметрии в точку .

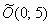Но работать гораздо удобнее с приведённым уравнением. Найдём фокусы:

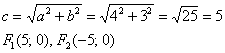
В случае перечисленных выше преобразований они как раз и «переезжают» в точки 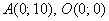условия задачи.

Вычислим эксцентриситет: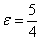

Date: 2015-04-23; view: 1582; Нарушение авторских прав