Поворот вокруг центра и параллельный перенос гиперболы

Вернёмся к демонстрационной гиперболе 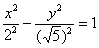. Что произойдёт, если в полученном уравнении поменять значения полуосей: 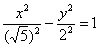? Для эллипса данный трюк означал поворот на 90 градусов. Но здесь всё иначе! Уравнение 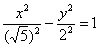определяет совершенно другую гиперболу. Ну, хотя бы обратите внимание на иные вершины: .

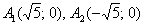Теперь рассмотрим уравнение 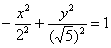, которое очевидно тоже задаёт гиперболу. Однако к исходному уравнению оно также не имеет никакого отношения! Это предыдущая гипербола, повёрнутая на 90 градусов, с вершинами 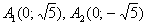на оси ординат.

И, наконец, оставшийся случай 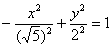задаёт нашу гиперболу 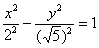, повернутую на 90 градусов. Как быть, если в практической задаче встретилась такая неканоническая запись?

Если требуется только построить кривую, то, наверное, лучше построить её в нестандартном виде. Это довольно просто. Уравнения асимптот гиперболы 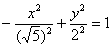обладают обратными угловыми коэффициентами:

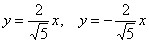
Поскольку оси «поменялись ролями», то вершины будут расположены на оси ординат в точках 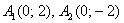. Выразим верхнюю ветвь гиперболы:

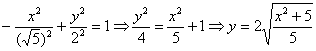
И найдём несколько дополнительных точек:

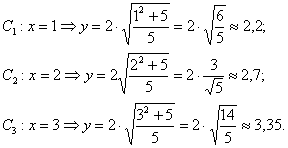
Выполним чертёж:

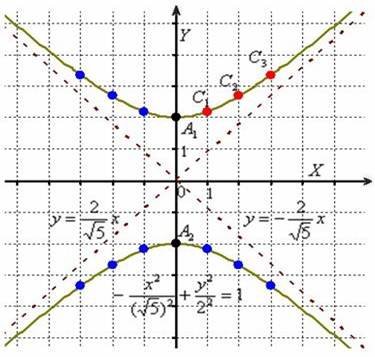
Помимо геометрии, похожие графики требуется строить в некоторых задачах математического анализа.

Однако по возможности всё-таки лучше осуществить поворот на 90 градусов и переписать уравнение 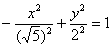в канонической форме. Для этого следует поменять местами значения полуосей и переставить «минус» к переменной «игрек»: .
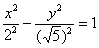И далее работать уже с каноническим уравнением.

! Примечание: строгий теоретический подход предполагает поворот координатных осей, а не самой линии. При необходимости оформляйте решение по аналогии с соответствующим примечанием предыдущего урока.

Параллельный перенос. Уравнение 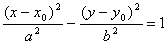задаёт гиперболу с действительной полуосью «а», мнимой полуосью «бэ» и центром в точке .

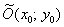Так, например, гипербола 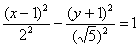имеет центр симметрии в точке 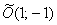. Асимптоты, само собой, переместились вместе с гиперболой, их уравнения отыскиваются по формулам:

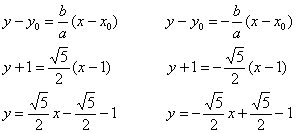
Полуоси 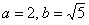и расстояние от фокусов до центра симметрии 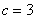остались прежними, а вот координаты фокусов изменились с учётом параллельного переноса:

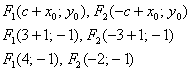
Параллельный перенос гиперболы доставил заметно больше хлопот, чем параллельный перенос эллипса, смотрим на картинку:

После таких трудов, уравнение трогать бессмысленно, но если таки просят, то придётся….

В нестрогом варианте: «Приведём уравнение гиперболы 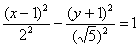к каноническому виду путём параллельного переноса в начало координат: ».

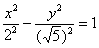Или в строгом – с параллельным переносом системы координат началом в точку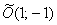
(см. шаблон у эллипса).

На практике часто встречается комбинация поворота на произвольный угол и параллельного переноса гиперболы. Данная ситуация рассматривается на уроке Приведение уравнения линии 2-го порядка к каноническому виду.

Date: 2015-04-23; view: 1347; Нарушение авторских прав