Определение гиперболы. Фокусы и эксцентриситет

У гиперболы, точно так же, как и у эллипса, есть две особенные точки 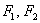, которые называются фокусами. Не говорил, но на всякий случай, вдруг кто неверно понимает: центр симметрии и точки фокуса, разумеется, не принадлежат кривым.

Общая концепция определения тоже похожа:

Гиперболой называют множество всех точек плоскости, абсолютное значение разности расстояний до каждой из которых от двух данных точек 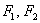– есть величина постоянная, численно равная расстоянию между вершинами этой гиперболы: 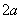. При этом расстояние между фокусами превосходит длину действительной оси: .

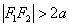Если гипербола задана каноническим уравнением 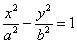, то расстояние от центра симметрии до каждого из фокусов рассчитывается по формуле: .
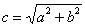И, соответственно, фокусы имеют координаты .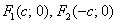

Для исследуемой гиперболы :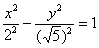

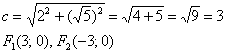
Разбираемся в определении. Обозначим через 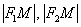расстояния от фокусов до произвольной точки 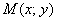гиперболы:

Сначала мысленно передвигайте синюю точку по правой ветви гиперболы – где бы мы ни находились, модуль (абсолютное значение) разности между длинами отрезков 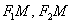будет одним и тем же:

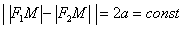
Если точку 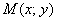«перекинуть» на левую ветвь, и перемещать её там, то данное значение останется неизменным.

Знак модуля нужен по той причине, что разность длин 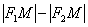может быть как положительной, так и отрицательной. Кстати, для любой точки правой ветви 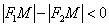(поскольку отрезок 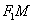короче отрезка 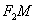). Для любой точки 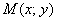левой ветви ситуация ровно противоположная и .

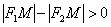Более того, ввиду очевидного свойства модуля 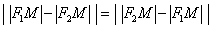безразлично, что из чего вычитать.

Удостоверимся, что в нашем примере модуль данной разности действительно равен расстоянию между вершинами. Мысленно поместите точку 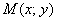в правую вершину гиперболы 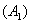. Тогда: 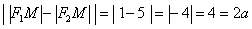, что и требовалось проверить.

Эксцентриситетом гиперболы называют отношение .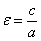

Так как расстояние от центра до фокуса больше расстояния от центра до вершины: 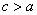, то эксцентриситет гиперболы всегда больше «единицы»: .

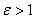Для данного примера: .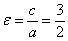

По аналогии с эллипсом, зафиксировав значение 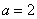, желающие могут провести самостоятельный анализ и проверку следующих фактов:

При увеличении эксцентриситета ветви гиперболы «распрямляются» к оси .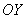
В предельном случае 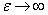они стремятся занять положение двух прямых, проходящих через точки 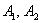параллельно оси ординат.

Если же значение эксцентриситета приближается к единице, то ветви гиперболы «сплющиваются» к оси .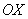

Date: 2015-04-23; view: 1063; Нарушение авторских прав