Смешанное произведение векторов в координатах

Способ расчёта смешанного произведения векторов чисто алгебраический:

Смешанное произведение векторов 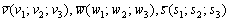, заданных в ортонормированном базисе 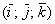правой ориентации, выражается формулой:

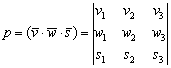
Определение, строго говоря, неполное, но в теоретические тонкости вникать не будем, правая ориентация базиса – это его «нормальная» ориентация, в которой мы будем решать практические задачи. Вполне достаточно.

В различных источниках на ваши головы выльют тонны различных свойств смешанного произведения. С практической точки зрения считаю важным отметить лишь некоторые вещи:

Как и для векторного произведения, координаты векторов следует «укладывать» в определитель в строгом порядке. Если в смешанном произведении 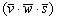выбрать два вектора (любых) и переставить их местами, то нужно переставить и соответствующие строки определителя. А по свойству определителя, при перестановке двух строк он меняет знак. Таким образом, при перестановке любых двух векторов смешанное произведение меняет знак.

Следует отметить, что координаты векторов не обязательно записывать в строки, их можно записать и в столбцы – слева направо, и тоже в строгом порядке:

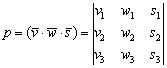
Значение определителя от этого не изменится (см. статью Свойства определителя и понижение его порядка). Дело вкуса.

Второй важный момент касается компланарности векторов. Как уже отмечалось, если векторы 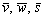компланарны, то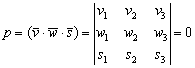

Такое задание уже было! В конце урока Линейная (не) зависимость векторов. Базис векторов мы разбирали задачу «доказать, что три вектора образуют базис пространства», где рассчитывали определитель третьего порядка и получали некоторое число. Так вот: по сути – мы находили смешанное произведение трёх векторов. И с геометрической точки зрения полученное число по модулю равнялось объёму параллелепипеда, построенного на данных векторах! Ну, а если получался ноль, то делали вывод, что векторы компланарны и базиса не образуют.

Закидываем остатки Буратино в огонь:

Пример 11

Даны векторы .

Вычислить:
а) смешанное произведение векторов;
б) объём параллелепипеда, построенного на векторах ;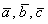
в) объём тетраэдра, построенного на векторах .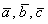

Решение: Всё быстро и просто:

а) По формуле смешанного произведения:

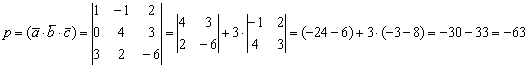
(Определитель раскрыт по первому столбцу)

б) Объём параллелепипеда, построенного на векторах 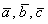, равен модулю смешанного произведения данных векторов:

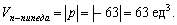
в) Вычислим объём тетраэдра, построенного на данных векторах:

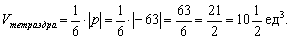
Ответ: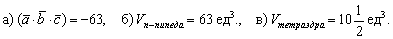

В пункте а) тоже можно было добавить размерность «кубические единицы», но здесь к объёму добавляется знак «минус», поэтому смотреться будет всё-таки не очень.

На практике, по моей субъективной оценке, в 95-99% случаев требуется вычислить объём треугольной пирамиды:

Пример 12

Вычислить объём треугольной пирамиды, если даны её вершины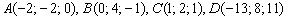

Решение: Чайникам рекомендую выполнить схематический рисунок пирамидки, чтобы лучше понять суть проводимых действий.

Сначала найдём векторы:

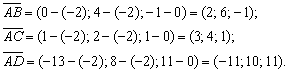
Вычислим смешанное произведение:

(Определитель раскрыт по первой строке)

Вычислим объём треугольной пирамиды :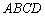

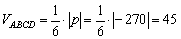
Ответ: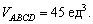

Рассмотренная задача имеет не единственное решение, можно было взять и другую группу векторов, начиная движуху от любой другой вершины пирамиды. Чем-то похоже на задачу предыдущей части урока о площади треугольника.

Объём тетраэдра – хит смешанного произведения, поэтому заключительный счастливый номер пусть будет таким же:

Пример 13

Вычислить объём пирамиды, заданной вершинами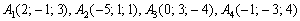

Это пример для самостоятельного решения. В образце решения рассмотрены векторы, отложенные от «традиционной» точки .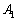

Остались только веселящие душу угольки, и в заключение хочу добавить, что в общем виде смешанное произведение векторов определено в аффинной системе координат. Более подробную информацию и формулы можно почерпнуть у тандема Атанасяна-Базылева.

Любите векторы, и векторы полюбят вас!

Решения и ответы:

Пример 2: Решение: По соответствующей формуле:

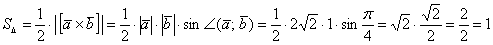
Ответ: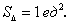

Пример 5: Решение:
1) Выразим вектор 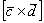через вектор :

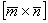2) Вычислим длину векторного произведения:

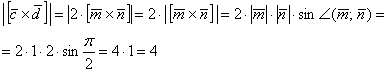
Ответ: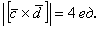

Пример 7: Решение: 1) Найдём векторное произведение:

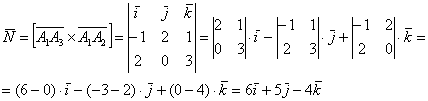
2) Вычислим длину векторного произведения:

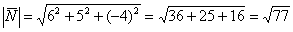
Ответ: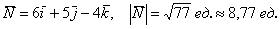

Пример 9: Решение: Найдём вектор:
.
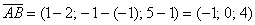Векторное произведение:

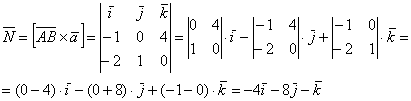
Площадь параллелограмма:

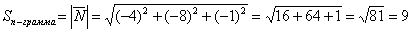
Ответ: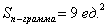

Пример 13: Решение: Найдём векторы:

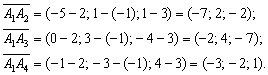
Вычислим смешанное произведение:

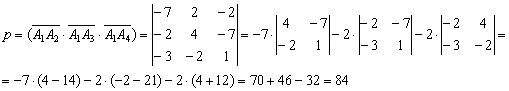
(Определитель раскрыт по первой строке)
Вычислим объём пирамиды :

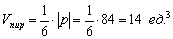
Ответ: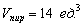

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Уравнение прямой на плоскости.
Направляющий вектор прямой. Вектор нормали

Прямая линия на плоскости – это одна из простейших геометрических фигур, знакомая вам ещё с младших классов, и сегодня мы узнаем, как с ней справляться методами аналитической геометрии. Для освоения материала необходимо уметь строить прямую; знать, каким уравнением задаётся прямая, в частности, прямая, проходящая через начало координат и прямые, параллельные координатным осям. Данную информацию можно найти в методичке Графики и свойства элементарных функций, я её создавал для матана, но раздел про линейную функцию получился очень удачным и подробным. Поэтому, уважаемые чайники, сначала разогрейтесь там. Кроме того, нужно обладать базовыми знаниями о векторах, иначе понимание материала будет неполным.

На данном уроке мы рассмотрим способы, с помощью которых можно составить уравнение прямой на плоскости. Рекомендую не пренебрегать практическими примерами (даже если кажется очень просто), так как я буду снабжать их элементарными и важными фактами, техническими приёмами, которые потребуются в дальнейшем, в том числе и в других разделах высшей математики.

Date: 2015-04-23; view: 1056; Нарушение авторских прав