Свойства векторного произведения векторов

Некоторые свойства векторного произведения мы уже рассмотрели, тем не менее, я их включу в данный список.

Для произвольных векторов 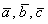и произвольного числа 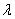справедливы следующие свойства:

1) 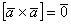В других источниках информации данный пункт обычно не выделяют в свойствах, но он очень важен в практическом плане. Поэтому пусть будет.

2) 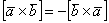– свойство тоже разобрано выше, иногда его называют антикоммутативностью. Иными словами, порядок векторов имеет значение.

3) 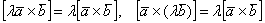– сочетательные или ассоциативные законы векторного произведения. Константы безпроблемно выносятся за пределы векторного произведения. Действительно, чего им там делать?

4) 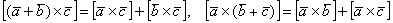– распределительные или дистрибутивные законы векторного произведения. С раскрытием скобок тоже нет проблем.

В качестве демонстрации рассмотрим коротенький пример:

Пример 3

Найти , если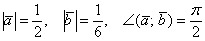

Решение: По условию снова требуется найти длину векторного произведения. Распишем нашу миниатюру:

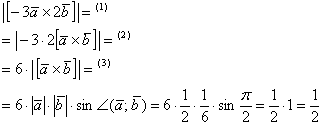
(1) Согласно ассоциативным законам, выносим константы за переделы векторного произведения.

(2) Выносим константу за пределы модуля, при этом модуль «съедает» знак «минус». Длина же не может быть отрицательной.

(3) Дальнейшее понятно.

Ответ: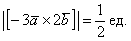

Пора подбросить дров в огонь:

Пример 4

Вычислить площадь треугольника, построенного на векторах 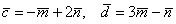, если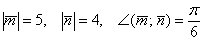

Решение: Площадь треугольника найдём по формуле 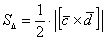. Загвоздка состоит в том, что векторы «цэ» и «дэ» сами представлены в виде сумм векторов. Алгоритм здесь стандартен и чем-то напоминает примеры №№3,4 урока Скалярное произведение векторов. Решение для ясности разобьём на три этапа:

1) На первом шаге выразим векторное произведение 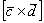через векторное произведение 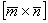, по сути, выразим вектор через вектор. О длинах пока ни слова!

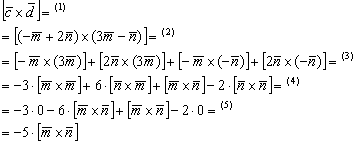
(1) Поставляем выражения векторов .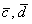

(2) Используя дистрибутивные законы, раскрываем скобки по правилу умножения многочленов.

(3) Используя ассоциативные законы, выносим все константы за пределы векторных произведений. При маломальском опыте действия 2 и 3 можно выполнять одновременно.

(4) Первое и последнее слагаемое равно нулю (нулевому вектору) благодаря приятному свойству 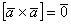. Во втором слагаемом используем свойство антикоммутативности векторного произведения: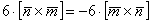

(5) Приводим подобные слагаемые.

В результате вектор оказался выражен через вектор, чего и требовалось достичь:

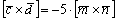
2) На втором шаге найдем длину нужного нам векторного произведения. Данное действие напоминает Пример 3:

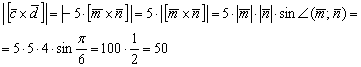
3) Найдём площадь искомого треугольника:

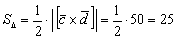
Этапы 2-3 решения можно было оформить и одной строкой.

Ответ: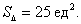

Рассмотренная задача достаточно распространена в контрольных работах, вот пример для самостоятельного решения:

Пример 5

Найти 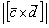, если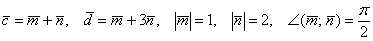

Краткое решение и ответ в конце урока. Посмотрим, насколько вы были внимательны при изучении предыдущих примеров;-)

Date: 2015-04-23; view: 1113; Нарушение авторских прав