Уравнение прямой с угловым коэффициентом

Всем известный «школьный» вид уравнения прямой 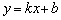называется уравнением прямой с угловым коэффициентом . Например, если прямая задана уравнением 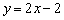, то её угловой коэффициент: 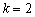. Рассмотрим геометрический смысл данного коэффициента и то, как его значение влияет на расположение прямой:

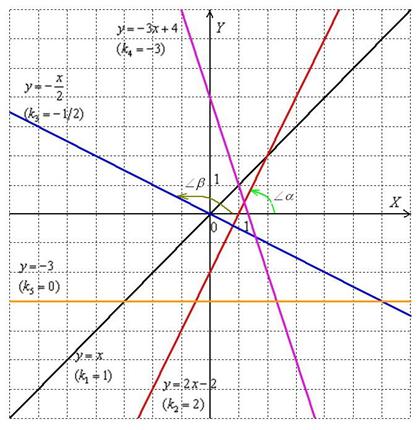
В курсе геометрии доказывается, что угловой коэффициент прямой равен тангенсу угла между положительным направлением оси 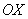и данной прямой: 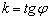, причём угол 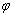«откручивается» против часовой стрелки.

Чтобы не загромождать чертёж, я нарисовал углы только для двух прямых. Рассмотрим «красную» прямую 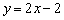и её угловой коэффициент 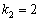. Согласно вышесказанному: 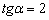(угол «альфа» обозначен зелёной дугой). Для «синей» прямой 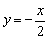с угловым коэффициентом 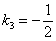справедливо равенство 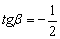(угол «бета» обозначен коричневой дугой). А если известен тангенс угла, то при необходимости легко найти и сам угол с помощью обратной функции – арктангенса. Как говорится, тригонометрическая таблица или микрокалькулятор в руки. Таким образом, угловой коэффициент характеризует степень наклона прямой к оси абсцисс.

При этом возможны следующие случаи:

1) Если угловой коэффициент отрицателен: 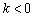, то линия, грубо говоря, идёт сверху вниз. Примеры – «синяя» и «малиновая» прямые на чертеже.

2) Если угловой коэффициент положителен: 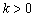, то линия идёт снизу вверх. Примеры – «чёрная» и «красная» прямые на чертеже.

3) Если угловой коэффициент равен нулю: 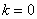, то уравнение 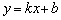принимает вид 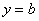, и соответствующая прямая параллельна оси 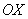. Пример – «жёлтая» прямая.

4) Для семейства прямых 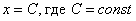, параллельных оси 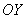(на чертеже нет примера, кроме самой оси 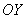), угловой коэффициент не определён. В данной ситуации 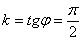, а тангенса угла 90 градусов не существует.

Чем больше угловой коэффициент по модулю, тем круче идёт график прямой.

Например, рассмотрим две прямые 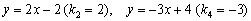. Здесь 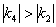, поэтому прямая 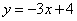имеет более крутой наклон. Напоминаю, что модуль позволяет не учитывать знак, нас интересуют только абсолютные значения угловых коэффициентов.

В свою очередь, прямая 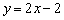более крутА, чем прямые .

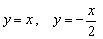Обратно: чем меньше угловой коэффициент по модулю, тем прямая является более пологой.

Для прямых 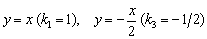справедливо неравенство 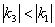, таким образом, прямая более полога. Детская горка, чтобы не насадить себе синяков и шишек.

Date: 2015-04-23; view: 1091; Нарушение авторских прав