Что получается в результате раскрытия определителя?

В результате получается ВЕКТОР. А как иначе? Векторное произведение – это же вектор.

Пример 6

Найти векторное произведение векторов 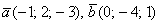и его длину.

Решение: Задача состоит из двух частей: во-первых, необходимо найти само векторное произведение (вектор), а во-вторых – его длину.

1) Найдём векторное произведение:

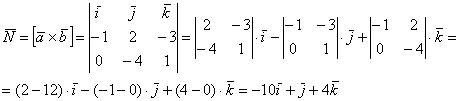
В результате получен вектор 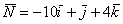, или, ещё можно записать .

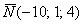Существует очень хороший способ проверки: как следует из определения, вектор 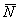должен быть ортогонален векторам . Ортогональность векторов, как мы разбирались, проверяется с помощью скалярного произведения:

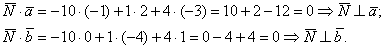
Если получилось хотя бы одно число, отличное от нуля, ищите ошибку в раскрытии определителя.

2) Вычислим длину векторного произведения. Используем простейшую формулу для вычисления длины вектора, которая рассматривалась на уроке Векторы для чайников:

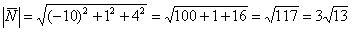
Ответ: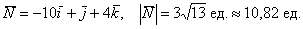

В плане технических обозначений здесь, наоборот, вместо громоздкой конструкции 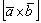выгодно использовать букву 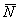, поскольку она сокращает запись

Аналогичный пример для самостоятельного решения:

Пример 7

Даны векторы 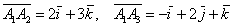. Найти 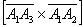и вычислить .

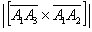Решение с ответом в конце урока. Будьте внимательны!

Огонь камина в самом разгаре, и самое время добавить живительный геометрический смысл в наши задачи:

Пример 8

Даны вершины треугольника 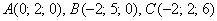. Найти его площадь.

Решение: Алгоритм решения, думаю, многие уже представляют. Сначала найдём векторы:

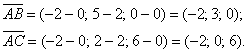
Затем векторное произведение:

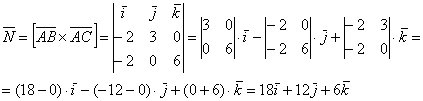
Вычислим его длину:

Формулы площадей параллелограмма и треугольника, само собой, остаются те же самые:

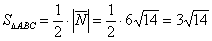
Ответ: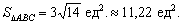

Рассмотренную задачу можно решить ещё двумя способами – было не обязательно выбирать стороны . Решение также допустимо провести через векторы 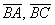либо . Желающие могут проверить, что во всех трёх случаях получится один и тот же ответ. Настоятельно рекомендую выполнить схематический рисунок, чтобы лучше понять вышесказанное.

Еще одна важная особенность состоит в том, что в задачах на нахождение площади фигуры порядок векторов не имеет значения. Действительно, если находить 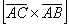, то получим противоположно направленный вектор 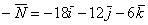, но формула вычисления длины вектора всё равно «съест» эти минусы. Заметьте, что такую перестановку нельзя делать в Примерах №№6,7, поскольку там требовалось найти вполне конкретный вектор.

Пример 9

Вычислить площадь параллелограмма, построенного на векторах 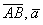, если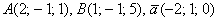

Это пример для самостоятельного решения.

В заключение первого раздела рассмотрим обещанную задачу урока Линейная (не) зависимость векторов. Базис векторов:

Пример 10

Проверить, будут ли коллинеарны следующие векторы пространства:
а)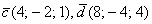
б)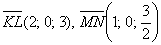

Решение: Проверка основана на одном из утверждений данного урока: если векторы коллинеарны, то их векторное произведение равно нулю (нулевому вектору): .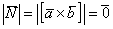

а) Найдём векторное произведение:

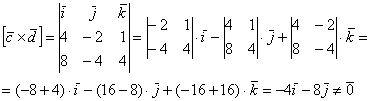
Таким образом, векторы 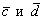не коллинеарны.

б) Найдём векторное произведение:

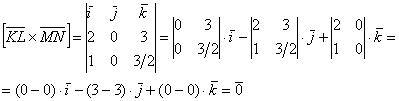
Значит,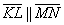

Ответ: а) не коллинеарны, б)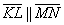

Вот, пожалуй, и все основные сведения о векторном произведении векторов.

Date: 2015-04-23; view: 1112; Нарушение авторских прав