Векторное произведение коллинеарных векторов

Определение подробно разобрано, осталось выяснить, что происходит, когда векторы коллинеарны. Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного параллелограмма равна нулю. Это же следует и из формулы – синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулевая

Таким образом, если 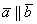, то 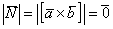. Строго говоря, само векторное произведение равно нулевому вектору, но на практике этим часто пренебрегают и пишут, что оно просто равно нулю.

Частный случай – векторное произведение вектора на самого себя:

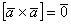
С помощью векторного произведения можно проверять коллинеарность трёхмерных векторов, и данную задачу среди прочих мы тоже разберём.

Для решения практических примеров может потребоваться тригонометрическая таблица, чтобы находить по ней значения синусов.

Ну что же, разжигаем огонь:

Пример 1

а) Найти длину векторного произведения векторов , если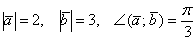

б) Найти площадь параллелограмма, построенного на векторах , если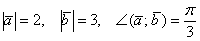

Решение: Нет, это не опечатка, исходные данные в пунктах условия я намеренно сделал одинаковыми. Потому что оформление решений будет отличаться!

а) По условию требуется найти длину вектора (векторного произведения). По соответствующей формуле:

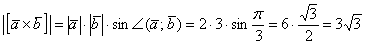
Ответ: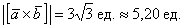

Коль скоро спрашивалось о длине, то в ответе указываем размерность – единицы.

б) По условию требуется найти площадь параллелограмма, построенного на векторах . Площадь данного параллелограмма численно равна длине векторного произведения:

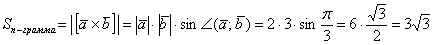
Ответ: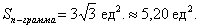

Обратите внимание, что в ответе о векторном произведении речи не идёт вообще, нас спрашивали о площади фигуры, соответственно, размерность – квадратные единицы.

Всегда смотрим, ЧТО требуется найти по условию, и, исходя из этого, формируем чёткий ответ. Может показаться буквоедством, но буквоедов среди преподавателей хватает, и задание с хорошими шансами вернётся на доработку. Хотя здесь не особо натянутая придирка, если ответ неточен, складывается впечатление, что человек плохо разобрался в материале и не вник в суть задания. Об этом желательно помнить, решая любую задачу по высшей математике, да и по другим предметам тоже.

Куда подевалась большая буковка «эн»? В принципе, её можно было дополнительно прилепить в решение, но в целях сократить запись, я этого не сделал. Надеюсь, всем понятно, что 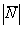и 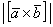– это обозначение одного и того же.

Популярный пример для самостоятельного решения:

Пример 2

Найти площадь треугольника, построенного на векторах , если

Формула нахождения площади треугольника через векторное произведение дана в комментариях к определению. Решение и ответ в конце урока.

На практике задача действительно очень распространена, треугольниками вообще могут замучить.

Для решения других задач нам понадобятся: