Ван-дер-ваальсовский газ

В п.1.8 отмечалось, что поведение реальных газов хорошо опи­сывается уравнением

pV_M =RT. (1.67)

только при малых плотностях, т. е. при не слишком больших дав­лениях и достаточно высоких температурах (см. (1.22)). С повыше­нием давления и уменьше­нием температуры наблю­даются значительные отсту­пления от уравнения. Во втором столбце: табл.1.2 приведены значения произ­ведения pV для массы азо­та, занимающей при нор­мальных условиях объем, равный одному литру. Ука­занные значения даны для различных давлений и одной и той же температу­ры 0°С.

P, атм	РV, а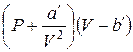тм×л	, атм×л
	1,000	1.000
	0.994	1.000
	1,048	1,009
	1.390	1,014
	2,069	0,893

В соответствии с уравнением (1.67) произведение pV при неиз­менной температуре должно оставаться постоянным. В действи­тельности, как видно из таблицы, при давлениях порядка 200 атм наблюдаются заметные отклонения, которые, непрерывно возра­стая с увеличением давления, достигают при 1000 атм более 100%.

Эти отклонения не представляются удивительными, поскольку при увеличении плотности начинают играть все большую роль объем молекул и взаимодействие между ними.

Для описания поведения газов в широком интервале плотностей было предложено много различных уравнений. Самым простым из них и вместе с тем дающим достаточно хорошие результаты оказа­лось уравнение Ван-дер-Ваальса. Это уравнение получено путем внесения поправок в уравнение (1.67) и имеет следующий вид:

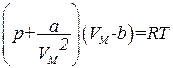, (1.68)

где p — давление, оказываемое на газ извне (равное давлению газа на стенки сосуда), а и b — константы Ван-дер-Ваальса, имею­щие для разных газов различные значения, определяемые опытным путем. Если давление выражено в паскалях, а объем— в куби­ческих метрах на моль, то константа а измеряется в Па×м⁶/моль², а константа b — в м³/моль. Иногда константу а выражают в атм·л²/моль² , а константу b — в л/моль.

Из-за взаимного притяжения между молекулами газ как бы сжимается большим давлением, чем давление p, оказываемое на газ стенками сосуда, в котором он заключен. Поправка харак­теризует ту добавку к внешнему давлению, которая обусловлена взаимным притяжением молекул друг к другу. Заметное воздей­ствие молекул друг на друга осуществляется в пределах небольших расстояний, называемых радиусом молекулярного действия. Сила взаимного притяжения двух элементарных объемов, имеющих размеры порядка этого радиуса, пропорцио­нальна как числу молекул заключенных в одном из объемов, так и числу молекул, заключенных в другом объеме. Каждое из этих чисел в свою очередь пропорционально числу молекул в единице объема, т.е. обратно пропорционально объему газа. Этими соображениями можно пояснить то обстоятельство, что поправка к давлению в (1.68) имеет вид 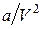. Вследствие того, что молекулы обладают конечным объемом, пространство, доступное для движения молекул, оказывается мень­шим, чем объем сосуда V _M. Поправка b в (1.68) характеризует ту часть объема, которая недоступна для движения молекул. Она равна нескольким суммарным объемам молекул, содержащихся в моле газа.

Уравнение (1.68) написано для одного моля газа. Чтобы перейти к уравнению для произвольной массы т, нужно учесть, что 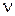молей газа при тех же условиях занимают в раз больший объем: V= n V _м.

Заменив в (1.68) V _м через V/ n, получим

.

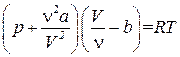Умножив это уравнение на v, и, введя обозначения

а'= n ²a, b'= n b, (1.69)

приходим к уравнению Ван-дер-Ваальса для v молей

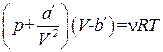. (1.70)

Буквам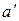и и обозначены константы Ван-дер-Ваальса для v молей. Их связь с а и b дается соотношениями (1.69). Константа а' измеряется в Па×м⁶, константа b' имеет размерность объема. Насколько уравнение Ван-дер-Ваальса лучше передает поведение газов, чем уравнение (1.67), можно судить по данным, приведенным в табл. 1.2. В третьем столбце таблицы даны значения величины 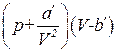[10] для той же массы азота, для которой даны во втором столбце значения рV. Как видно из таблицы, урав­нение Ван-дер-Ваальса гораздо лучше согласуется с экспериментом, чем уравнение (1.67).

В соответствии с тем фактом, что все реальные газы с умень­шением плотности приближаются по своим свойствам к идеаль­ному газу, уравнение Ван-дер-Ваальса в пределе, при стремлении объема к бесконечности, переходит в уравнение (1.67). В этом можно убедиться, вынеся в уравнении (1.70) р и V за скобки

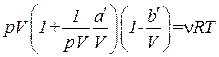
и приняв во внимание, что произведение pV остается примерно постоянным.

Реальные газы следуют уравнению Ван-дер-Ваальса лишь приближенно. Воображаемый газ, точно подчиняющийся уравне­нию (1.68), называется Ван-дер-ваальсовским.

Внутренняя энергия Ван-дер-ваальсовского газа должна включать в себя, кроме кинетической энергии молекул, энергию взаимодействия между молекулами. Для нахождения внутренней энергии Ван-дер-ваальсовского газа воспользуемся тем обстоятельством, что работа, совершаемая при расширении газа, против сил взаимного притяжения молекул друг к другу, равна приращению энергии взаимодействия: d'A=dE_p. Силы взаимного притяжения между молекулами учтены в уравнении (1.68) с помощью добавки к давлению, равной a/V² _М Соответственно работа против сил взаимодействия между молекулами может быть представлена в виде 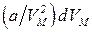(подобно этому работа, совершаемая газом против внешних сил, определяется выражением РdV). Таким образом,

.

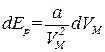Интегрирование этого выражения дает, что

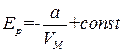. (1.71)

Внутренняя энергия ван-дер-ваальсовского газа зависит как от объема, так и от температуры. Следовательно, выражение для U _м имеет вид:

(мы включили const выражения (1.69) в f(T)). Это выражение в пределе при стремлении объема к бесконечности должно перехо­дить в выражение (1.28) для внутренней энергии идеального газа. Следовательно, f(T)=С_VT.

Итак, внутренняя энергия моля ван-дер-ваальсовского газа определяется формулой

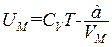. (1.72)

Внутренняя энергия 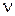молей будет в 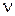раз больше:

(1.73)

(мы учли, что v²a=a' и vV _м =V). По формулам (1.72) и (1.73) можно находить приближенные значения внутренней энергии реальных газов.

Date: 2015-05-05; view: 966; Нарушение авторских прав