Политропические процессы

Политропическими называются процессы, при которых теплоемкость тела остается постоянной. Таким образом, условие, которое выполняется в ходе политропического процесса, заключается в том, что

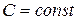. (1.44)

Найдем уравнение политропы для идеального газа. Напишем уравнение первого начала (1.13) для одного моля газа, представив δ Q в виде CdT, а dU – в виде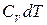

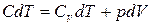. (1.45)

В полученное уравнение входят все три параметра: p, V и T. Один из них можно исключить с помощью уравнения состояния. Чтобы получить уравнение политропы сразу в переменных p и V, исключим T. Для этого продифференцируем соотношение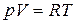

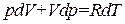. (1.46)

Исключив из уравнений (1.45) и (1.46) dT и произведя приведение подобных членов, получим

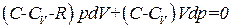. (1.47)

Заменив 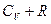через 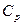(см. (1.33)) и разделив (1.47) на pV, придем к дифференциальному уравнению

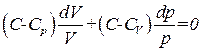. (1.48)

Величины C, и 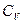являются константами. Поэтому интегрирование уравнения (1.48) приводит к соотношению

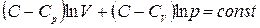. (1.49)

Разделив это соотношение на 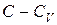(что возможно, если 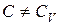) и, произведя потенцирование, получим

, (1.50)

где

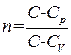. (1.51)

Уравнение (1.50) и есть искомое уравнение политропы идеального газа для случая, когда 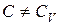. Величина n в (1.51) называется показателем поли-тропы.

Процесс	n
Изобарический
Изотермический
Адиабатический	γ
Изохорический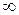

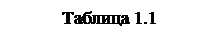Чтобы установить характер политропического процесса при 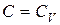, обратимся к уравнению (1.49). При 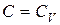это уравнение принимает вид 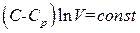, откуда следует, что V в ходе процесса остается постоянным. Таким образом, политропический процесс с 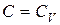является изохорическим процессом. Это можно было предвидеть заранее, поскольку 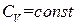и представляет собой теплоемкость при постоянном объеме, т. е. при изохорическом процессе. Согласно (1.51) показатель политропы при изохорическом процессе стремится к бесконечности.

Остальные рассмотренные в предыдущем параграфе процессы также относятся к категории политропных процессов. Изобарическому процессу соответствует 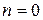(см. (1.50)), изотермическому – 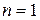и, наконец, адиабатическому – 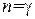. Значения показателя политропы n для перечисленных процессов даны в табл. 1.1.

Решив уравнение (1.51) относительно C, получим формулу для теплоемкости идеального газа при политропическом процессе

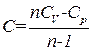. (1.52)

Подстановка 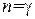обращает выражение (1.52) в нуль (при проверке этого утверждения нужно принять во внимание формулу (1.35)). Следовательно, теплоемкость идеального газа при адиабатическом процессе равна нулю. При адиабатическом процессе теплоемкость равна нулю для всех тел. Это вытекает из того, что при адиабатическом процессе 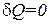, в то время как dT отличен от нуля.

Подстановка 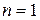обращает выражение (1.52) в бесконечность. Таким образом, при изотермическом процессе теплоемкость бесконечно велика. Это объясняется тем, что при изотермическом процессе 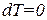, в то время как 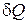отличен от нуля.

Date: 2015-05-05; view: 822; Нарушение авторских прав