Скорость звука в газах

В механике известна следующая формула для скорости распространения звука в газах:

, (1.62)

где ρ – плотность газа. Но давление Р зависит не только от ρ, а также и от температуры Т. Поэтому надо указать, в каком смысле понимается производная dP/d ρ. Ньютон считал, что давление связано с плотностью законом Бойля-Мариотта: Р /ρ= сonst. Это соответствует предположению, что разности температур между сгущениями и разряжениями воздуха в звуковой волне мгновенно выравниваются, так что распространение звука есть изотермический процесс. Если это верно, то под dP/d ρ следует понимать частную производную (dP/d ρ) _Т. Тогда формула (1.62) перейдёт в формулу Ньютона

, (1.63)

где µ – молярная масса газа, а индекс N указывает, что с_N - скорость звука, вычисленная по формуле Ньютона. Полагая для воздуха µ = 28,8 г/моль, Т = 73 К, получаем по формуле (1.63) с_N = 280 м/с, тогда как опыт даёт с = 330 м/с.

Расхождение было устранено Лапласом (1749-1827). Он указал, что колебания плотности и связанные с ними колебания температуры в звуковой волне происходят настолько быстро, а теплопроводность настолько мала, что для таких процессов теплообмен не играет никакой роли. Разности температур между сгущениями и разряжениями воздуха в звуковой волне не успевают выравниваться, так что распространение звука можно считать адиабатическим процессом. В таком случае надо пользоваться не уравнением изотермы, а уравнением адиабаты (1.42). Если в это уравнение вместо объема ввести плотность ρ ~ 1/ V, то оно перейдёт в

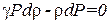, (1.64)

откуда для адиабатического процесса

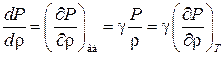. (1.65)

Поэтому вместо формулы Ньютона получаем формулу Лапласа

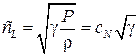. (1.66)

Она даёт для скорости звука величину в 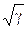раз больше, чем формула Ньютона. Измерения γ для воздуха привели к результату γ = 1,4. Поэтому согласно формуле Лапласа при Т = 273 К скорость звука в воздухе должна быть 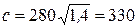м/с, что согласуется с опытом.

На формулах Ньютона и Лапласа основан удобный метод экспериментального измерения отношений теплоёмкостей γ. Экспериментально измеряется скорость звука с в исследуемом газе. Значение γ вычисляется по формуле

,

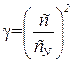где с_N – так называемая ньютонова скорость звука, т. е. величина, определяемая формулой (1.63). Величина же, определяемая формулой (1.66), называется лапласовой скоростью звука.

Date: 2015-05-05; view: 1697; Нарушение авторских прав