Контрольная работа № 1

Задача № 1. Заданы матрицы А, В, С. Найти: а) (3 А + 2 В) С;
б) det A. Данные, соответствующие вашему варианту, брать в таблице.

Вариант	А	В	С

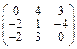
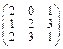
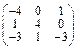
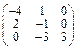
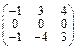
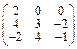
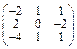
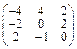
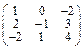
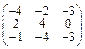
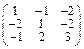
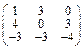
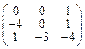
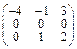
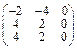
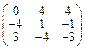
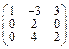
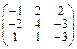
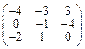
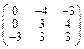
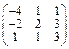
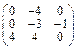
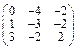
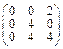
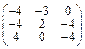
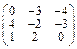
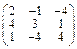
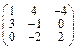
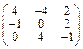
Задача № 2. Для матрицы А найти: а) 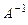; б) 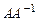; в) решить систему матричным методом. Данные, соответствующие вашему варианту, брать в таблице.

Вариант	А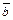

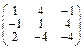
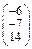
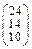
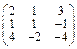
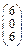
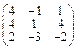
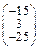
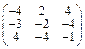
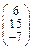
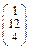
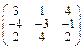
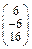
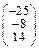
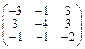
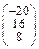
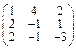
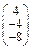
Задача № 3. Решить систему уравнений методом Крамера. Данные, соответствующие вашему варианту, брать в таблице.

Вариант	Система

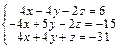
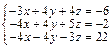
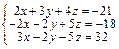
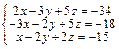
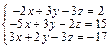
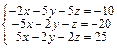
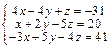
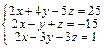
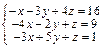
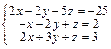
Задача № 4. Исследовать совместность систем, для совместной системы найти решение. Данные, соответствующие вашему варианту, брать в таблице.

Вариант	а	б

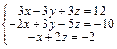
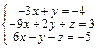
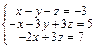
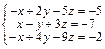
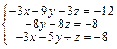
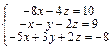
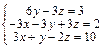
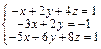
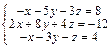
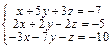
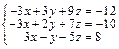
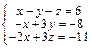
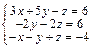
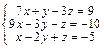
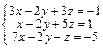
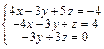
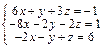
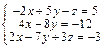
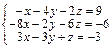
Задача № 5. Даны вершины пирамиды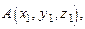

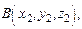
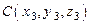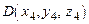, . Найти: а) угол между векторами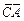
и ; б) площадь грани АВС; в) проекцию вектора 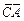на вектор 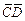; г) объем пирамиды; д) длину высоты пирамиды, опущенной из вершины D. Данные, соответствующие вашему варианту, брать в таблице.

Вариант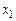

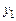
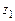
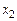
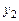
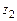
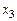
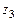
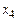
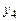
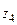
–6

–2

–1

–1

–2

–1

–1

–2

–1

–1

Контрольная работа № 2

Задача № 1. Даны вершины пирамиды 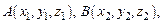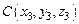, . Найти: а) угол между гранями АВС и АВD; б) каноническое и параметрические уравнения прямой CD; в) уравнение плоскости, параллельной плоскости АВС, проходящей через точ-
ку D; г) каноническое уравнение высоты пирамиды. Данные, соответствующие вашему варианту, брать в таблице.

Вариант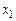

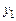
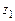
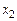
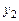
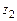
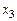
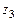
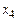
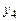
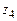
–6

–2

–1

–1

–2

–1

–1

–2

–1

–1

Задача № 2. Даны три точки на плоскости: 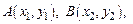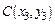. Найти: а) уравнение стороны АВ; б) уравнение высоты, опущенной из вершины А; в) уравнение медианы, опущенной из вершины В; г) уравнение прямой, параллельной прямой ВС, проходящей через точку А; д) угол при вершине В. Сделать чертеж. Данные, соответствующие вашему варианту, брать в таблице.

Вариант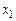
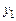
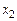
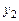
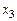
		–2			–11
				–4	–2	–1
			–12	–9	–5
		–2			–12
			–4	–5	–8	–2
		–5			–11
	-6	–4	–10	–1
					–4

Задача № 3. Привести уравнение кривой второго порядка 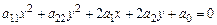к каноническому виду, выяснить, что это за кривая. Найти координаты смещенного центра. Построить кривую на плоскости. Данные, соответствующие вашему варианту, брать в таблице.

Вариант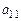
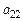
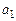
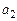
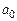
				–6	–50
		–4			–20
	–1				–12
					–45
					–100
			–2	–3	–35
	–2				–30
					–54
					–49
			–15	–12	–30

Список литературы

1. Гусак А.А. Высшая математика. Т. 1: Учебник для студентов вузов. – Минск: Тетра Система, 2000. – 544 с.

2. Бугров Я.С., Никольский С.М. Высшая математика: элементы линейной алгебры и аналитической геометрии. – М.: Наука, 1984. – 382 с.

3. Гусак А.А. Справочное пособие к решению задач: аналитическая геометрия и линейная алгебра. – Минск, 1998.

4. Беклемешев Д.В. Курс аналитической геометрии и линейной алгебры. – М.: Наука, 1980.

5. Ильин В.А., Позняк Э.Г. Аналитическая геометрия. – М., 1981.

6. Ильин В.А., Позняк Э.Г. Линейная алгебра. – М., 1978.

7. Ефимов Н.В. Краткий курс аналитической геометрии. – М., 1975.

Date: 2015-04-23; view: 586; Нарушение авторских прав