Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Пример 1. В ПДСК даны векторы Найти единичный вектор х, перпендикулярный векторам а, b
|
|
В ПДСК даны векторы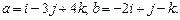 
Найти единичный вектор х, перпендикулярный векторам а, b.
Решение. Вектор с = а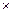 
b перпендикулярен векторам а, b.
c = a 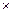b = 
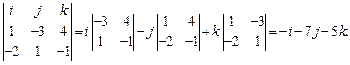
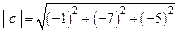
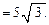В качестве вектора х можно взять
вектор х = 
или вектор х =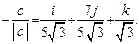 
Векторы a, b,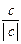 
образуютправую тройку векторов, а a, b, 
левую.
Ответ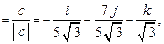: х 
или х 
Пример 2
Найти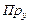 
х если известно, что х = а + 2 b, у= 2 а – b, 
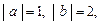угол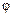 
между векторами а, b равен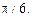 
Решение. 
Используя свойства скалярного произведения, находим
(х, у) = (а + 2 b, 2 a – b) = 2 (a, a) + 3 (a, b) – 2 (b, b) =
= 
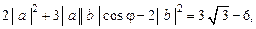
= ( 2 a – b, 2 a – b) = 4 (a, a) – 4 (a, b) + (b, b) =
= 
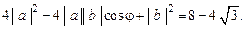
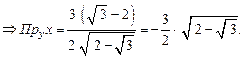
Ответ: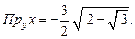 
Пример 3
В ПДСК заданы векторы a = i + 3j – k, b = -i – j + k, c = 2i – j + 3k. Найти вектор х такой, чтобы его скалярное произведение с векторами a, b, c равнялось –12, 6, –8 соответственно.
Решение. Пусть х =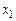 
i + 
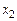j +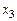 
k. Из условия задачи получаем
(а, х) = 
(b, x) = – 
(с, х) = 
Необходимо решить систему линейных алгебраических уравнений с неизвестными 
По формуле Крамера находим
Ответ: x = -4i – 3j – k.
Date: 2015-04-23; view: 911; Нарушение авторских прав