Гипербола

Гиперболой называется множество всех точек плоскости, разность расстояний от которых до двух фиксированных точек, называемых фокусами, есть величина постоянная.

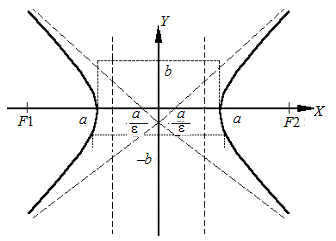
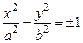– каноническое уравнение гиперболы,

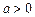– действительная полуось,

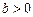– мнимая полуось,

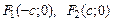– левый и правый фокусы,

,

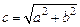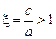– эксцентриситет,

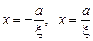– левая и правая директриса,

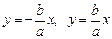– асимптоты гиперболы.

Парабола

Параболой называется множество всех точек плоскости, равноудаленных от фиксированной точки, называемой фокусом и от данной прямой, называемой директрисой.

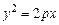– каноническое уравнение параболы,

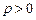– фокальный параметр,

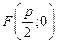– фокус,

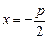– директриса.

Пример

Найти уравнение геометрического места точек, отношение расстояний которых от точки F (4; 0) и от прямой х = 25/4 равно 4/5.

Решение. Возьмем произвольную точку Р (х, у), удовлетворяющую условию задачи. На прямой 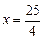возьмем точку 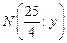. Длина вектора 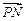равна расстоянию от точки Р до прямой 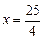, а длина вектора 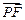равна расстоянию от точки Р до точки 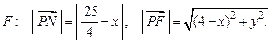Из условия задачи находим:

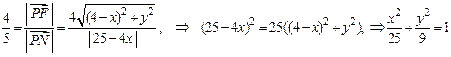– эллипс.

Ответ: – эллипс.

Date: 2015-04-23; view: 574; Нарушение авторских прав