Рассмотрим систему линейных алгебраических уравнений

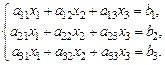Назовем матрицу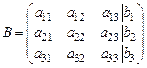

расширенной матрицей системы, которая получается добавлением к матрице А столбца свободных членов 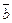. Найдем и 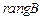, где А – основная матрица системы.

Если: 1) 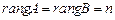, где n – число неизвестных в системе, то система имеет одно решение;

2) 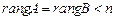, система имеет бесконечное множество решений;

3) 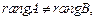система не имеет решений.

В тех случаях, когда система имеет одно или множество решений, по «треугольному» виду расширенной матрицы восстанавливаем систему и решаем ее снизу вверх.

Пример

Исследовать совместность систем:

а) 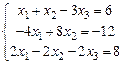; б) 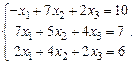Решить совместную систему.

Решение

а) Запишем расширенную матрицу системы и с помощью цепочки элементарных преобразований приведем ее к «треугольному» виду. 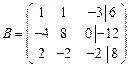~ (умножим первую строку на 4 и сложим со
второй строкой. Затем умножим первую строку на (–2) и сложим
с третьей) ~ 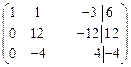~ (поменяем местами вторую и третью строки матрицы) ~ 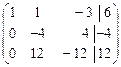~ (умножим вторую строку на 3 и сложим с третьей) ~ 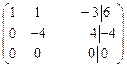. Получим матрицу

в «треугольном» виде. Найдем ранги основной и расширенной матрицы. В «треугольном» виде расширенной матрицы две ненулевых строки, следовательно, rangB = 2. «Треугольный» вид основной матрицы

получаем из «треугольного» вида расширенной матрицы отбрасыванием

последнего столбца, стоящего за чертой 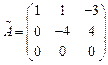, здесь также две ненулевые строки – rangA = 2.

Так как rangA = rangB = 2 < 3, система имеет бесконечное множество решений. Найдем их, для чего восстановим систему по «треуголь-ному» виду расширенной матрицы. 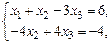из последне-
го уравнения найдем 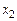и подставим в первое уравнение

.

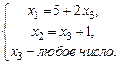б) Запишем расширенную матрицу системы и с помощью цепочки элементарных преобразований приведем ее к «треугольному» виду. 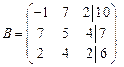~ (умножим первую строку на 7 и сложим со второй, затем на 2 и сложим с третьей) ~ 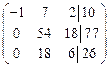~ (поменяем местами вторую и третью строки) ~ 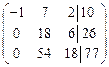~ (умножим вторую строку на (–3) и сложим с третьей) ~ 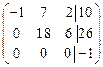. Найдем ранги основной и расширенной матрицы. В «треугольном» виде расширенной матрицы три ненулевых строки, следовательно, rangВ = 3. «Треугольный» вид основной матрицы получаем из «треугольного» вида расширенной матрицы отбрасыванием последнего столбца, стоящего за чертой, 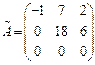, здесь две ненулевые строки – rangA = 2. Так как rangA ≠ rangВ, система не имеет решений.

Ответ: а) 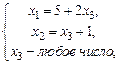б) система не имеет решений.

Date: 2015-04-23; view: 599; Нарушение авторских прав