Линейных алгебраических уравнений

Матрица 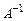называется обратной по отношению к квадратной матрице А, если 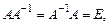где 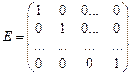– единичная матрица.

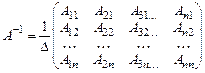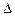Обратная матрица существует для всякой квадратной матрицы, определитель которой отличен от нуля, , где – определитель матрицы А, 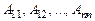– алгебраические дополнения соответствующих элементов матрицы А. Алгебраические дополнения находятся по формуле:

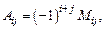
где 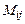– определитель, полученный вычеркиванием в определителе матрицы A i -й строки и j -го столбца, называемый минором.

Пусть дана система линейных алгебраических уравнений:

Матрица 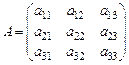называется основной матрицей системы.

Вектор – матрица 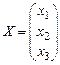называется матрицей неизвестных. Вектор – матрица 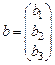называется матрицей правых частей. Тогда исходную систему можно переписать в виде АХ = b. Решение этой системы находится по формуле Х = А^-1 b.

Пример

Решить систему уравнений матричным методом:

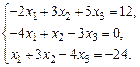
Решение. Найдем определитель основной матрицы системы

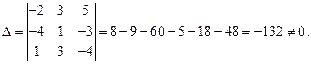
Так как определитель отличен от нуля, существует обратная матри-
ца А ^–1. Для нахождения обратной матрицы находим все алгебраические дополнения:

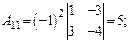
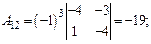
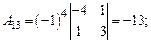
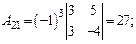
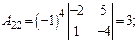
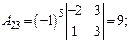
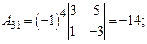
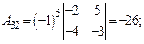
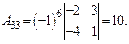
Тогда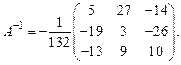

Решение системы 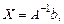где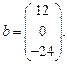

.

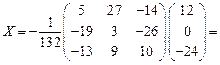
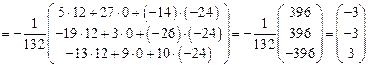Ответ: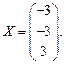

1.1.5. Ранг матрицы. Решение систем

Date: 2015-04-23; view: 535; Нарушение авторских прав