Внутренняя энергия и теплоемкости идеального газа. Теорема Больцмана о распределении энергии по степеням свободы

Внутренняя энергия и теплоемкость идеального газа.

Чтобы изменить состояние некоторого заданного объема газа (например, нагреть или охладить его), надо либо совершить над ним механическую работу, либо передать ему некоторое количество тепла за счет контакта с другими телами. Количественно эти изменения выражаются с помощью первого начала термодинамики, которое отражает важнейший закон природы: сохранение механической и тепловой энергии тела. Формулировку первого начала для бесконечно малого квазистатического процесса можно представить в виде (см. ТЕРМОДИНАМИКА).

(13) dQ = dU + dA

Здесь dQ – элементарное количество тепла, передаваемое телу, dU – изменение его внутренней энергии, dA = pdV – элементарная работа, совершаемая газом при изменении его объема (эта работа равна с обратным знаком элементарной работе, совершаемой внешними силами над газом). Обозначение dU соответствует полному дифференциалу от переменной U. Это означает, что приращение внутренней энергии при переходе газа из некоторого состояния 1 в состояние 2 можно представить в виде интеграла

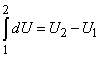
Обозначения dQ и dA означают, что в общем случае интеграл от них нельзя представить в виде разности соответствующих значений в конечном и начальном состоянии газа, поэтому интегрирование (13) по всему процессу приводит к соотношению

Q = U2 – U1 + A

Вводится понятие теплоемкости газа как количества тепла, которое нужно сообщить газу, чтобы повысить его температуру на один градус Кельвина. Тогда по определению

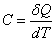
Далее под С подразумевается теплоемкость, отнесенная к одному молю газа, или молярная теплоемкость. Внутренняя энергия U также определена для одного моля газа. Если газ нагревается при постоянном объеме (изохорический процесс), т.е. совершаемая газом работа равна нулю, то

(14)

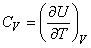
Если состояние газа меняется при постоянном давлении (изобарический процесс), то в соответствии с (13)

(15)

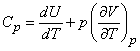
Использование уравнение состояния идеального газа (3) при v = 1 дает

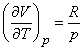
Следовательно, молярные теплоемкости идеального газа при постоянном давлении и при постоянном объеме связаны соотношением

(16) Cp = Cv + R

Внутренняя энергия газа, в общем случае, состоит из кинетической энергии поступательного и вращательного движения молекул, энергии внутреннего (колебательного) движения атомов в молекуле, а также потенциальной энергии взаимодействия молекул. В случае идеального газа вкладом последнего слагаемого в полную энергию можно пренебрегать.

В классической статистической механике доказывается так называемая теорема о равномерном распределении кинетической энергии по степеням свободы молекул, согласно которой на каждую степень свободы молекулы в состоянии теплового равновесия в среднем приходится энергия, равная (1/2)kT.

Для газов, состоящих из одноатомных молекул, (например, инертные газы) средняя кинетическая энергия, приходящаяся на один атом, определена соотношением (7), поскольку она соответствует лишь поступательному движению атомов, (3 степени свободы). В этом случае

,

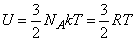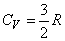
Существенно, что для идеального газа одноатомных молекул внутренняя энергия зависит только от температуры и не зависит от объема.

Для линейных двухатомных молекул число степеней свободы равно пяти (на одну степень свободы меньше, чем для системы двух независимых атомов, поскольку в молекуле эти атомы связаны жесткой связью) Дополнительные две степени свободы описывают вращательное движение молекулы относительно двух взаимно-перпендикулярных осей. При этом

,

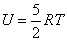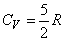
Если атомы в молекуле совершают еще и колебания, то, согласно классической теории, наличие колебательного движения вносит вклад в среднюю энергию молекулы, равный kT (по kT/2, приходящийся на кинетическую и потенциальную энергии колебаний. Тогда в случае молекулы, образованной из атомов,

,

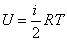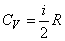
где i = nпост + nвращ + 2nкол – полное число степеней свободы молекулы. При этом nпост = 3. Для линейной молекулы nвращ = 2, nкол = 3N – 5. Для всех других молекул nвращ = 3, nкол = 3N – 6.

Классическая теория, в основном, правильно описывает тепловые явления в газе в некоторых узких интервалах температур, однако температурная зависимость теплоемкости в целом, наблюдаемая в эксперименте, ведет себя далеко не так, как предсказывает классическая теория. Это несоответствие теории и эксперимента было понято только с появлением квантовой теории теплоемкости, основанной на представлении о дискретности вращательных и колебательных уровней молекул. При низких температурах наблюдается только поступательное движение молекул. С ростом температуры все большее число молекул вовлекается во вращательное движение. Если средняя тепловая энергия kT заметно превышает энергию первого вращательного уровня, в молекуле возбуждено уже много вращательных уровней. В этом случае дискретность уровней становится несущественной и теплоемкость равна своему классическому значению. Аналогичная ситуация имеет место и с возбуждением колебательных степеней свободы. Квантовая теория полностью объясняет характер температурной зависимости теплоемкости, ее непрерывный характер, отличающийся постепенным вовлечением в «игру» различных степеней свободы молекул.

Изотермические и адиабатические процессы в газе. Наряду с процессами изменения параметров газа, происходящими при постоянном объеме или при постоянном давлении, возможны изотермические (T = const, внутренняя энергия газа остается неизменной) и адиабатические (без отвода и подвода тепла к газу) процессы. В первом случае все подводимое к газу тепло расходуется на механическую работу, а изменение давления и объема для одного моля газа удовлетворяет условию pV = PT = const. В p-V координатах на плоскости соответствующие зависимости образуют семейство изотерм.

Для адиабатического процесса (dQ = 0) из (13) и (14) следует

CVdT + pdV = 0

Уравнение состояния идеального газа дает

dT = R–1(pdV + Vdp).

Используя (16), уравнение адиабатического процесса можно представить в дифференциальной форме

(17) gpdv + Vdp = 0, где g = Ср/CV – отношение теплоемкостей при постоянном давлении и постоянном объеме, называемое адиабатической постоянной. Дифференциальному соотношению (17) при g = const соответствует уравнение адиабаты pVg = const

или

(18) TVg – 1 = const

Так как g > 1, то из (18) следует, что при адиабатическом сжатии газ нагревается, а при расширении – охлаждается. Это явление находит применение, например, в дизельных двигателях, где горючая смесь воспламеняется за счет адиабатического сжатия.

В статистической физике выводится закон Больцмана о равномерном распределении энергии по степеням свободы молекул: для статистической системы, которая находится в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная kT/2, а на каждую колебательную степень свободы — в среднем энергия, равная kT. Колебательная степень обладает вдвое большей энергией, т.к. на нее приходится как кинетическая энергия (как в случае поступательного и вращательного движений), так и потенциальная, причем средние значения потенциальной и кинетической и энергии одинаковы. Значит, средняя энергия молекулы

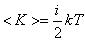
средняя энергия приходящаяся на одну степень свободы: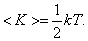

У одноатомной молекулы i = 3, тогда для одноатомных молекул

для двухатомных молекул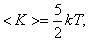

для трёхатомных молекул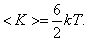

11. C = Q / m delta T; C = dQ/ dTm;
Cm = dQ / dT МЮ – молярная теплоемкость. В газе различают теплоемкости при постоянном давлении и теплоемкость при постоянном объеме.
1) V=const; dV=0; dA=PdV=0; dQ=dU; Ev = dQm / dT; Eт = dUm / dT;
Um = i k T Na/ 2 = i R T / 2; где i – число степеней свободы;
dUm = i R dT / 2; Ev = i R / 2 – теплоемкость при постоянном V;
2) P = const; dAm = dm + dA; dA= pdV; PV=RT; PdV= RdT;
dQm = Cv dT + RdT = Cv + RdT; Cp = dQm / dT= Cv +R; Cp= Cv +R - уравнение Майера; Cp = (iR / 2) + R = ((i +2)/ 2) R; Cp = ((i+2) / 2) R;
? = Cp / Cv = (i+2) / i – коэффециент Пуассона
Из полученной формулы видно, что теплоемкость газа не зависит от температуры. Эксперементально было установленно, что этот закон соблюдается в достаточно широком интервале температур только для одноатомных газов. Уже для простых молекул – молекул H2 зависимость Cv от температуры имеет вид: Cv = i R / 2 (рисунок – график, ступеньки; оси T, Cv). Такая зависимость теплоемкости от температуры обусловлена тем, что в случае простейшей молекулы нарушается принцип равновестного распределения энергии по степеням свободы. Вращательное и колебательное движение молекул квантуются, т.е. энергия вращательных и колебательных движений не может принимать любые значения, а может иметь только вполне определенные дискретные значения. При низких температурах энергии не достаточно, чтобы возбудить вращательное и колебательное движения молекул, поэтому вращательные и колебательные степени свободы “выморожены” и не участвуют в создании теплоемкости, поэтому при низких температурах молекулы H2 имеют только 3 степени свободы (поступ.) и Cv= 3R / 2. При увеличении температуры возбуждается сначало вращательное движение (i = 5, Cv = 5 R / 2), а затем при достаточно высокой температуре и колебательном движении (i =7, Cv = 7R / 2), т.е. число степеней свободы зависит от температуры.

. Классическая теория теплоемкости основана на предположении, что к атомно-молекулярным системам применимы законы классической ньютоновой механики. В действительности применимость ньютоновой механики к атомно-молекулярным системам ограничена. По этой причине классическая теория не смогла дать полного удовлетворительного решения проблемы теплоемкости и была заменена более общей квантовой теорией. Однако во многих случаях классическая теория приводила к удивительно хорошему согласию с опытом. Причина этого в том, что классическая теория является приближенным предельным случаем квантовой и, следовательно, имеет определенную область применимости. В пределах этой области выводы классической теории практически не отличаются от выводов квантовой. Мы начинаем изложение с классической теории. Она проще квантовой. При таком порядке изложения отчетливее выявятся принципиальные затруднения классической физики, преодоление которых привело к замене классических представлений квантовыми.
Для классических систем справедлива теорема о равномерном распределении кинетической энергии по степеням свободы. На основе этой теоремы можно построить классическую теорию теплоемкостей газов и твердых тел. Начнем с теплоемкости газов. В § 24 было показано, что для идеальных газов

cv = v Cp = v£i- (66-1)

Отсюда видно, что адиабатическая постоянная у однозначно определяет обе теплоемкости СР и Cv идеального газа. Поэтому для сопоставления теории с опытом достаточно сравнивать между собой опытные и теоретические значения только адиабатической постоянной у.
Внутренняя энергия газа состоит из кинетической энергии поступательного, вращательного и внутреннего движения молекул и атомов, а также из потенциальной энергии их взаимодействия. Для идеальных газов, когда молекулярные силы пренебрежимо малы, потенциальной энергией взаимодействия молекул можно пренебречь.

13. Основные понятия термодинамики.

I. Энергия

Понятие энергии – одно из основных физических понятий и потому не

имеет исчерпывающего определения. Для наших целей примем, что энергия -

это такая характеристика движения и взаимодействия тел, которая связана с

их способностью совершать изменения в состоянии системы и внешней

среды. Видов энергии очень много – механическая, тепловая,

электромагнитная, ядерная и т.д. Каждая из них может только

видоизменяться, т.е. превращаться в другие виды энергии.

Основные понятия и определения

Определение: Термодинамика – наука о закономерностях превращения энергии. В термодинамике широко используется понятие термодинамической системы.

Определение: Термодинамической системой называется совокупность материальных тел, взаимодействующих, как между собой, так и с окружающей средой. Все тела находящиеся за пределами границ рассматриваемой системы называются окружающей средой. Поскольку одно и тоже тело, одно и тоже вещество при разных условиях может находится в разных состояниях, (пример: лед – вода – пар, одно вещество при разной температуре) вводятся, для удобства, характеристики состояния вещества – так называемые параметры состояния.

Перечислим основные параметры состояния вещества:

Температура тел - определяет направление возможного самопроизвольного перехода тепла между телами. В Северной Америке используется шкала Фаренгейта. Для термодинамических расчетов очень удобна абсолютная шкала или шкала Кельвина. За ноль в этой шкале принята температура абсолютного нуля, при этой температуре прекращается всякое тепловое движение в веществе. Численно один градус шкалы Кельвина равен одному градусу шкалы Цельсия. В настоящее время в мире существует несколько температурных шкал и единиц измерения температуры. Наиболее распространенная в Европе шкала Цельсия где нулевая температура – температура замерзания воды при атмосферном давлении, а температура кипения воды при атмосферном давлении принята за 100 градусов Цельсия (° С).

Температура, выраженная по абсолютной шкале, называется абсолютной температурой.

Соотношение для перехода от градусов Цельсия к градусам Кельвина:

T [K] = t [°C] + 273.15

где: T - температура в Кельвинах, t – температура в градусах Цельсия.

Давление - представляет собой силу, действующею по нормали к поверхности тела и отнесенную к единице площади этой поверхности.

Для измерения давления применяются различные единицы измерения. В стандартной системе измерения СИ единицей служит Паскаль (Па).

Соотношение между единицами:

1 бар = 10⁵ Па

1 кг/см² (атмосфера) = 9.8067×10⁴ Па

1мм рт. ст (миллиметр ртутного столба) = 133 Па

1 мм вод. ст. ( миллиметр водного столба) = 9.8067 Па

Плотность – отношение массы вещества к объему занимаемому эти веществом.

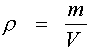
Удельный объем - величина обратная плотности т.е. отношения объема занятого веществом к его массе.

(

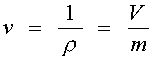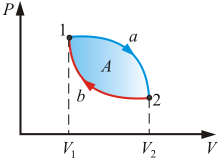
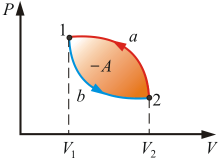
Прежде чем переходить к изложению второго закона термодинамики, рассмотрим круговые процессы. Круговым процессом, или циклом, называется такой процесс, в результате которого термодинамическое тело возвращается в исходное состояние. В диаграммах состояния P, V и других круговые процессы изображается в виде замкнутых кривых (рис. 5.1). Это связано с тем, что в любой диаграмме два тождественных состояния (начало и конец кругового процесса) изображаются одной и той же точкой на плоскости.

Цикл, совершаемый идеальным газом, можно разбить на процессы расширения (1 – 2) и сжатия (2 – 1) газа. Работа расширения (определяется площадью фигуры 1 a2V₂V₁ 1) положительна (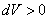), работа сжатия (определяется площадью фигуры 2 b1V₁V₂ 2) отрицательна (d V < 0). Следовательно, работа, совершаемая за цикл, определяется площадью, охваченной замкнутой кривой. Если за цикл совершается положительная работа

.

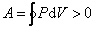(5.1.1)

(цикл протекает по часовой стрелке), то он называется прямым (рис. 5.1). Если за цикл совершается отрицательная работа

.

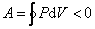(5.1.2)

(цикл протекает против часовой стрелки), то он называется обратным (рис. 5.2).

Круговые процессы лежат в основе всех тепловых машин: двигателей внутреннего сгорания, паровых и газовых турбин, паровых и холодильных машин и т. д.

В результате кругового процесса система возвращается в исходное состояние, и следовательно полное изменение внутренней энергии газа равно нулю. Поэтому первое начало термодинамики для кругового процесса

.

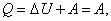(5.1.3)

т.е. работа, совершаемая за цикл, равна количеству полученной извне теплоты. Однако в результате кругового процесса система может теплоту как получать, так и отдавать, поэтому

.

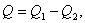(5.1.4)

где Q₁ – количество теплоты, полученное системой; Q₂ – количество теплоты, отданное системой.

Поэтому термический коэффициент полезного действия для кругового процесса

.

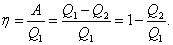(5.1.5)

Все термодинамические процессы, в том числе и круговые, делят на две группы: обратимые и необратимые.

Процесс называют обратимым, если он протекает таким образом, что после окончания процесса он может быть проведен в обратном направлении через все те же промежуточные состояния, что и прямой процесс. После проведения кругового обратимого процесса никаких изменений в среде, окружающей систему, не произойдет. При этом под средой понимается совокупность всех не входящих в систему тел, с которыми система непосредственно взаимодействует.

Процесс называется необратимым, если он протекает так, что после его окончания систему нельзя вернуть в начальное состояние через прежние промежуточные состояния. Нельзя осуществить необратимый круговой процесс, чтобы нигде в окружающей среде не осталось никаких изменений.

Свойством обратимости обладают только равновесные процессы. Каждое промежуточное состояние является состоянием термодинамического равновесия, нечувствительного к тому, идет ли процесс в прямом или обратном направлении.

Например, обратимым можно считать процесс адиабатического расширения или сжатия газа. При адиабатическом процессе условие теплоизолированности системы исключает непосредственный теплообмен между системой и средой. Поэтому, производя адиабатическое расширение газа, а затем сжатие, можно вернуть газ в исходное состояние так, что в окружающей среде никаких изменений не произойдет. Конечно, в реальных условиях, и в этом случае, всегда имеется некоторая необратимость процесса, обусловленная, например, несовершенством теплоизоляции, трением при движении поршня и т.д.

Только в обратимых процессах теплота используется по назначению, не расходуется зря. Если процесс неравновесный, то будет необратимый переход, т.е. часть энергии уйдет (необратимо).

Максимальным КПД обладают машины, у которых только обратимые процессы.

Реальные процессы сопровождаются диссипацией энергии (из-за трения, теплопроводности и т.д.), которая нами не рассматривается. Обратимые процессы – это в какой-то степени идеализация реальных процессов. Их рассмотрение важно по двум причинам:

• многие процессы в природе и технике практически обратимы;
• обратимые процессы являются наиболее экономичными и приводят к максимальному значению термического коэффициента полезного действия тепловых двигателей.