Третье начало термодинамики

(Нернста теорема)- закон термодинамики, согласно к-рому энтропия S равновесной системы стремится к конечному пределу, не зависящему от давления, плотности, др. термодинамич. параметров или фазы, при стремлении темп-ры к абс. нулю. Установлено экспериментально В. Нернстом (W. Nernst 1906). Т к. т. справедливо, напр., для всех чистых кристаллич. веществ, квантовых жидкостей и газов. Согласно второму началу термодинамики, энтропия определяется лишь с точностью до постоянного слагаемого So В 1911 М. Плате (М. Plank) предложил принять состояние при О К за начальное и считать, что т. с. S0 = 0. Тогда энтропия любого состояния определяется однозначно как а б с о л ю т н а я э н т р о п и я. Определение Планка удобно с точки зрения квантовой механики, к-рая тогда позволяет однозначно определить значения хим. констант (константы равновесия хим. реакций), что выходит за пределы формальной термодинамики.

Температурная зависимость разностей энтальпии DH свободной энергии DG и теплоёмкостей С Р, С V.

Нернст установил свою теорему, используя теорию хим. сродства к хим констант (см. Химическая термодинамика). Хим. сродство определяется макс. работой где DG -разность Гиббса энергий (ф-ций темп-ры и давления) реагирующих веществ и удовлетворяет термодинамич. соотношению где DH -разность энтальпий реагирующих веществ. Член TDS при низких темп-pax очень мал, особенно в реакциях с участием конденсированных фаз. На этом основано п р а в и л о Б е р т л о, согласно к-рому теплота реакций, идущих самопроизвольно, положительна. Однако когда преобладает член TDS это правило несправедливо и реакция может быть эндотермической. Теорема Нернста состоит в предположении, что при стремлении абс. темп-ры к нулю обращается в нуль не только TDS, но и DS. Отсюда с использованием Гиббса - Гельмгольца уравнения следует, что обращаются в нуль теплоёмкости при пост. давлении С Р и пост. объёме Cv;

Из Т, к. т. следует, что кривые должны иметь горизонтальную касательную при (рис.).

Т. к. из второго начала термодинамики следует, а, согласно Т. н. т., то при коэф. теплового расширения и изохорный коэф. давления стремятся к нулю. Т. н. т. не применимо к веществам, к-рые не находятся в состоянии полного статистич. равновесия, напр. к аморфным телам (см. Аморфное состояние)или неупорядоченным сплавам, к-рые могут существовать и при очень низких темп-pax как "замороженные" метастабильные состояния с очень большим временем жизни. Сомнения в справедливости Т. н. т. высказывались в связи с его неприменимостью к подобным веществам. Статистич. механика квантовых систем проясняет физ. смысл теоремы Нернста. П р и н ц и п Б о л ь ц м а н а в формулировке Планка связывает энтропию со статистическим весом состояния W соотношением

При

если осн. состояние невырождено, то Однако, как показано X. Крамерсом (Н. A. Kramers) и X. Казимиром (Н. В. Casimir), дискретность уровней лишь косвенно связана со стремлением энтропии к нулю. Даже если осн. уровень вырожден и но термодинамический пределто можно считать, что S0 = 0. Для макроскопич. тел квантовые уровни расположены чрезвычайно плотно и расстояние между ними стремится к нулю в термодинамич. пределе. Влияние дискретности квантовых уровней на поведение энтропии при стремлении темп-р к нулю могло бы быть обнаружено лишь при очень низких темп-pax, не достижимых экспериментально. Наблюдаемое поведение энтропии проявляется при гораздо более высоких темп-pax (когда длина волны де Бройля, соответствующая энергии ср. теплового движения частиц, становится сравнимой со ср. расстоянием между ними) и связано с явлением квантового вырождения газов и жидкостей

ТЕРМОДИНАМИКА НЕРАВНОВЕСНЫХ ПРОЦЕССОВ

общая теория макроскопич. описания неравновесных процессов. Её наз. также неравновесной термодинамикой или термодинамикой необратимых процессов.

Классич. термодинамика даёт полное количеств. описание равновесных (обратимых) процессов. Для неравновесных процессов она устанавливает лишь неравенства, к-рые указывают возможное направление этих процессов. Осн. задача Т. н. п.— количеств. изучение неравновесных процессов для состояний, не сильно отличающихся от равновесного, в частности определение скоростей неравновесных процессов в зависимости от внеш. условий.

В Т. н. п. системы, в к-рых протекают неравновесные процессы, рассматриваются как непрерывные среды, а их параметры состояния — как полевые переменные, т. е. непрерывные ф-ции координат и времени. Для макроскопич. описания неравновесных процессов применяют след. метод: систему представляют состоящей из элем. объёмов (элементов среды), к-рые всё же настолько велики, что содержат очень большое число ч-ц. Состояние каждого выделенного элемента среды характеризуется темп-рой, давлением и др. термодинамич. параметрами, зависящими от координат и времени. Количеств. описание неравновесных процессов при таком методе заключается в составлении ур-ний баланса для элем. объёмов на основе законов сохранения массы, импульса и энергии, а также ур-ния баланса энтропии и феноменологич. ур-ний рассматриваемых процессов, выражающих потоки массы, импульса и энергии через градиенты термодинамич. параметров. Методы Т. н. п. позволяют сформулировать для неравновесных процессов 1-е и 2-е начала термодинамики в локальной форме (зависящей от положения элемента среды); получить из общих принципов, не рассматривая деталей вз-ствия ч-ц, полную систему ур-ний переноса, т. е. ур-ния гидродинамики, теплопроводности и диффузии для простых и сложных систем (с хим. реакциями между компонентами, с учётом эл.-магн. сил и др. факторов).

Закон сохранения массы в Т. н. п.

Для многокомпонентной системы скорость увеличения массы k-той компоненты в элем. объёме равна потоку массы в этот объём rkvk, где rk — плотность, а vk — массовая скорость потока ч-ц данного вида. Поток в бесконечно малый элемент объёма, приходящийся на ед. объёма, есть дивергенция с обратным знаком; следовательно, ур-ние баланса массы k-той компоненты имеет вид: дrk/дt=-divrkvk. Для суммарной плотности r=Skrk закон сохранения имеет аналогичный вид:

дp/дt=-divrv,

где v—.гидродинамич. скорость среды (ср. скорость переноса массы), зависящая от координат и времени. Для концентрации к.-л. компонента ck=rk/r закон сохранения массы r(dck/dt)=-divJk позволяет определить диффуз. поток Jk=rk(v-v) (здесь d/dt=д/дt+v•grad— полная, или субстанциональная, производная во времени).

Закон сохранения импульса в Т. н. <п.

Изменение импульса элем. объёма может происходить за счёт сил, вызванных градиентом внутр. напряжений в среде Pab, и внеш. сил Fk,. Закон сохранения импульса, применённый к гидродинамич. скорости, позволяет получить осн. ур-ния гидродинамики (Навье — Стокса уравнения):

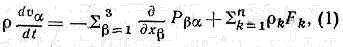
где va — декартовы компоненты скорости v, а Рba — тензор напряжений. Закон сохранения энергии для элем. объёмов представляет собой первое начало термодинамики в Т. н. п. Здесь приходится учитывать, что полная уд. энергия складывается из уд. кинетич., уд. потенц, энергии в поле сил Fk, и уд. внутр. энергии и, к-рая представляет собой энергию теплового движения ч-ц и ср. энергию вз-ствия ч-ц. Для и получается ур-ние баланса, аналогичное (1), из к-рого следует, что скорость изменения плотности импульса на одну ч-цу дru/дt определяется дивергенцией потоков внутр. энергии put? и потока теплоты Jq, а также работой внутр. напряжений

SabPab(дva/дxb) и внеш. сил SkJkFk.

Уравнение баланса энтропии.

В Т. н. п. принимается, что энтропия элем. объёма s (локальная энтропия) явл. такой же ф-цией от внутр. энергии и, уд. объёма v=1/r и концентрации сk, как и в состоянии полного равновесия, и, следовательно, для неё справедливы обычные термодинамич. равенства. Эти положения вместе с законами сохранения массы, импульса и энергии позволяют найти ур-ние баланса энтропии:

rds/dt= -divJs+s, (2)

где s — локальное производство энтропии на ед. объёма в ед. времени, Js — плотность потока энтропии, к-рая выражается через плотности потока теплоты, диффуз. потока и ту часть тензора напряжений, к-рая связана с неравновесными процессами (т. е. через тензор вязких напряжений Пaab). Энтропия (в отличие от массы, энергии и импульса) не сохраняется, а возрастает со временем в элементе объёма вследствие необратимых процессов (скорость возрастания обозначают о). Кроме того, энтропия может изменяться вследствие втекания её в элемент объёма или вытекания из него, что не связано с необратимыми процессами. Положительность произ-ва энтропии (s>0) выражает в Т. н. п. закон возрастания энтропии (см. ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ). Произ-во энтропии 0 определяется только необратимыми процессами (напр., диффузией, теплопроводностью, вязкостью) и равно:

s=SiJiXi, (3)

где Ji — потоки (напр., диффуз. поток Jk, тепловой поток Jq, тензор вязких напряжений Пab), а Xi—сопряжённые им термодинамич. силы, т. е. градиенты термодинамич. параметров, вызывающие отклонение от равновесного состояния. Для получения в Т. н. п. замкнутой системы ур-ний, описывающих неравновесные процессы, потоки физ. величин при помощи феноменологич. ур-ний выражают через термодинамич. силы.

Феноменологические уравнения.

Т. н. п. исходит из того, что при малых отклонениях системы от термодинамич. равновесия возникающие потоки линейно зависят от термодинамич. сил и описываются феноменологич. ур-ниями типа

Ji=SkLikXk, (4)

где Lik — кинетические (феноменологич.) коэффициенты, или коэфф. переноса. В прямых процессах термодинамич. сила Xk вызывает поток Jk, напр. градиент темп-ры вызывает поток теплоты (теплопроводность), градиент концентрации — поток в-ва (диффузию), градиент скорости — поток импульса (к-рый определяет вязкость), электрич. поле — электрич. ток (электропроводность). Такие процессы характеризуются кинетич. коэфф., пропорциональными коэфф. теплопроводности, диффузии, вязкости, электропроводности. Эти коэфф. наз. также кинетич. коэфф. или коэфф. переноса. Термодинамич. сила Хk может вызывать поток Ji и при i?k; напр., градиент темп-ры может вызывать поток в-ва в многокомпонентных системах (термодиффузия, или Соре эффект), а градиент концентрации — поток теплоты (диффуз. термоэффект, или Дюфура эффект). Такие процессы наз. перекрёстными или налагающимися эффектами; они характеризуются коэфф. Lik с i?k. С учётом феноменологич. ур-ний произ-во энтропии равно:

s=Si,kXiLikXk?0. (5)

В стационарном состоянии величина s минимальна при заданных внеш. условиях, препятствующих достижению равновесия (Пригожина теорема). В состоянии термодинамич. равновесия s=0. Одна из осн. теорем Т. н. п.— Онсагера теорема. В рассмотренных примерах термодинамич. параметры были непрерывными ф-циями координат. Возможны неравновесные системы, в к-рых термодинамич. параметры меняются скачком (гетерогенные системы), напр. газы в сосудах, соединённых капилляром или мембраной. Если темп-ры Т и химические потенциалы m газов в сосудах не равны (T1>T2 и m1>m2)> то термодинамич. силы (Xn=1/T2-1/T1, Xm=m2/T2-m1/T1) вызывают потоки массы и энергии (Jm=L11Xm+L12Xn, Jn=L21Xm+L22Xn) между сосудами, создают термомолекулярную разность давлений. В этом примере потоки и термодинамич. силы — скаляры; такие процессы наз. скалярными. В процессах диффузии, теплопроводности, термодиффузии и эффекте Дюфура потоки и термодинамич. силы — векторы, поэтому они наз. векторными процессами. В вязком потоке, при сдвиговой вязкости, термодинамич. силы и потоки — тензоры, поэтому этот процесс наз. тензорным. Согласно теореме франц. физика П. Кюри, для изотропной среды линейные соотношения могут связывать термодинамич. силы и потоки лишь одинаковой тензорной размерности, что сильно упрощает феноменологич. ур-ния в этом случае.

Т. н. п. даёт теор. основу для исследования открытых систем, позволяет объяснить мн. неравновесные явления в проводниках, напр. термоэлектрические явления, гальваномагнитные явления и термогальваномагнитные явления. Вывод законов Т. н. п. из законов механики (классич. и квантовой) и получение выражений для кинетич. коэфф. через параметры, характеризующие строение в-ва, входят в задачу неравновесной статистич. термодинамики. к-рая относится к Т. н. п. как статистич. термодинамика к термодинамике.