Применение 1-го начала термодинамики к изопроцессам и адиабатическому процессу

1) V = const изохорный => dV=0; d = PdV=0; dQ=dU; dU = МЮ dUмол = МЮ Cv dT;

dQ= МЮ Cv dT; Q = (интеграл T1 – T2) МЮ Cv dT = МЮ Cv (T2 – T1) – m Cv (T2 – T1)/ μ

^ 2) T = const изотермический => dT= 0; dQ= МЮ Cv dT = 0; dQ = dA;

dA = PdV; PV = МЮ RT; P= МЮ RT / V; dA = МЮ RT dV / V;

A = (интеграл V1 – V2) МЮ RTdV / V = МЮ RT (интеграл V1 – V2) dV/ V = МЮ RT ln (V2/ V1) = МЮ RT ln (P1/ P2); P1 V1 = P2 V2;

^ 3) P = const изобарический => dQ = PdV; A = (интеграл V1 – V2) PdV = P (V2 – V1); A = P (V2 – V1); dU = МЮ Cv dT; PdV = МЮ RdT; dQ = МЮ Cv dT + МЮ Rdt = МЮ (Cv + R) dT; Q = МЮ Cp (T2 – T1);

^ 4) Q = const Адиабатный dA = dU; dA = МЮ Cv dT; PdV = - МЮ Cv dT; PV = МЮ RT – продифференцированное уравнение Менделеева-Клайперона; PdV + VdP = МЮ R dT; …; lnP = - γ lnP + const; γ – коэффициент Пуассона; lnP + lnV (ст. γ) = const; PV (ст. γ ) = const; (график такой же как и изотермический, только чуть выше вверх).

dA = - dU = - МЮ Cv dT; A = - (интеграл T1 – T2) МЮ Cv dT = МЮ Cv (T1 – T2);

16. Карно цикл, обратимый круговой процесс, в котором совершается превращение теплоты в работу (или работы в теплоту). К. ц. состоит из последовательно чередующихся двух изотермических и двух адиабатных процессов. Впервые рассмотрен французским учёным Н. Л. С. Карно (1824) как идеальный рабочий цикл теплового двигателя. Превращение теплоты в работу сопровождается переносом рабочим телом двигателя определённого количества теплоты от более нагретого тела (нагревателя) к менее нагретому (холодильнику).

К. ц. осуществляется следующим образом: рабочее тело (например, пар в цилиндре под поршнем) при температуре T₁ приводится в соприкосновение с нагревателем, имеющим постоянную температуру T₁, и изотермически получает от него количество теплоты d Q₁ (при этом пар расширяется и совершает работу). На рис. 1 этот процесс изображен отрезком изотермы AB. Затем рабочее тело, расширяясь адиабатически (по адиабате BC), охлаждается до температуры T₂. При этой температуре, сжимаясь изотермически (отрезок CD), рабочее тело отдаёт количество теплоты d Q ₂ холодильнику с температурой T₂. Завершается К. ц. адиабатным процессом (DA на рис. 1), возвращающим рабочее тело в исходное термодинамическое состояние. При постоянной разности температур (T ₁ — T ₂) между нагревателем и холодильником рабочее тело совершает за один К. ц. работу

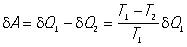
Эта работа численно равна площади ABCD (рис. 1), ограниченной отрезками изотерм и адиабат, образующих К. ц.

К. ц. обратим, и его можно осуществить в обратной последовательности (в направлении ADCBA). При этом количество теплоты d Q₂ отбирается у холодильника и вместе с затраченной работой d А (превращенной в теплоту) передаётся нагревателю. Тепловой двигатель работает в этом режиме как идеальная холодильная машина.

К. ц. имеет наивысший кпд h =d A/ d Q ₁ = (T₁ — T ₂)/ T ₁ среди всех возможных циклов, осуществляемых в одном и том же температурном интервале (T ₁ — T₂). В этом смысле кпд К. ц. служит мерой эффективности др. рабочих циклов.

Исторически К. ц. сыграл важную роль в развитии термодинамики и теплотехники. С его помощью была доказана эквивалентность формулировок Р. Клаузиуса и У. Томсона (Кельвина) второго начала термодинамики, К. ц. был использован для определения абсолютной термодинамической шкалы температур (см. Температурные шкалы), К. ц. часто использовался также для вывода различных термодинамических соотношений (например, Клапейрона — Клаузиуса уравнения).

Date: 2015-05-04; view: 1034; Нарушение авторских прав