
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Уравнение Клейна-Гордона-Фока и волновая функция фотона
|
|
Уравнение Шредингера описывает нерелятивистскую микрочастицу. Чтобы получить уравнение для волновой функции релятивистской частицы, воспользуемся релятивистской связью энергии и импульса:
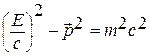
и подставим в нее выражения для квадрата энергии и импульса, полученные с помощью производных из волновой функции 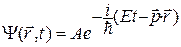 и аналогичные выражениям
и аналогичные выражениям
E = 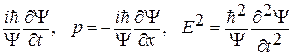 , p 2 = –
, p 2 = – 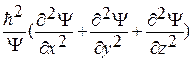 .
.
Приходим к дифференциальному уравнению Клейна-Гордона-Фока, которое аналогично уравнению Шредингера, но описывает волновую функцию свободной релятивистской частицы:
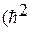 „ + m2c2)
„ + m2c2) 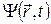 ,
,
где дифференциальный оператор „ = 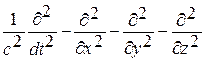 – оператор д¢Аламбера.
– оператор д¢Аламбера.
Пусть фотон движется со скоростью света с. Он не имеет массы покоя. Фотон может быть по-разному поляризован в пространстве, то есть, его волновая функция должна быть векторной функцией. В пространстве Минковского волновая функция фотона образует 4-вектор 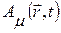 . «Временная» часть этого вектора связана с потенциалом j электрического поля: A ct = j / c, а «пространственная» часть
. «Временная» часть этого вектора связана с потенциалом j электрического поля: A ct = j / c, а «пространственная» часть 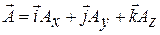 называется вектор-потенциалом.
называется вектор-потенциалом. 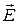 – напряженность электрического поля,
– напряженность электрического поля, 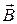 – индукция магнитного поля:
– индукция магнитного поля:
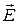 =– grad j = ¶
=– grad j = ¶ 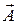 /¶ t,
/¶ t, 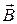 = rot
= rot 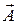 .
.
Имеем для фотона:
„ Am = 0 Û 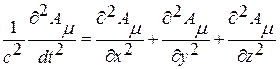 .
.
Это стандартное уравнение (волновое). Аналогичные волновые уравнения справедливы для электрического и магнитного полей:
„ 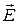 = 0 и „
= 0 и „ 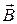 = 0.
= 0.
* Уравнение квантовой теории для свободного фотона совпадает по форме с классическим уравнением, описывающим электромагнитную волну.
Пусть поле, в котором находится релятивистская частица, потенциально и стационарно. Тогда к полной энергии частицы, определяемой соотношением
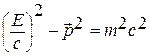 ,
,
Надо добавить энергию взаимодействия с внешним полем:
E = 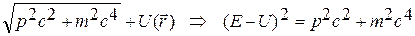 .
.
Подставляя последние выражения в (**) и учитывая 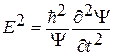 и
и
p 2 = – 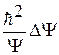 , получим стационарное уравнение, позволяющее найти волновую функцию y релятивистской частицы во внешнем потенциальном поле:
, получим стационарное уравнение, позволяющее найти волновую функцию y релятивистской частицы во внешнем потенциальном поле:
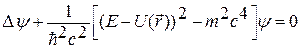 .
.
Date: 2015-06-08; view: 954; Нарушение авторских прав