Принцип неопределенности. В квантовой физике понятия определенного местоположения и траектории микрочастиц теряют смысл

В квантовой физике понятия определенного местоположения и траектории микрочастиц теряют смысл. Эти понятия применимы к микрочастицам только с некоторой степенью точности.

Степень точности, с какой к частицам может быть применено представление об определенном ее положении в пространстве, дается соотношением неопределенностей, установленное Гейзенбергом. Согласно этому соотношению частица не может иметь одновременно вполне точные значения, например, координаты x и соответствующей ей составляющей импульса p_x, причем неопределенности в значениях этих величин удовлетворяют условию:

D x × D p_x ³ . (*)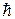

Такая запись означает, что произведение неопределенностей координаты и соответствующего ей импульса может быть меньше величины порядка 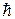. Чем точнее определена одна из величин, тем больше становится неопределенность другой. Возможны состояния частицы, когда одна из величин имеет вполне точное значение, тогда вторая величина будет совершенно неопределенной.

Соотношения (*) справедливы для любой другой координаты и соответствующего ей импульса, а также для ряда других величин, например, для взятых попарно проекций момента количества движения на координатные оси.

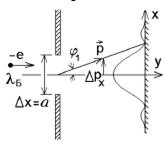Поясним соотношение неопределенностей. Для определения положения микрочастицы (она летит свободно) поставим на ее пути щель шириной D x, расположенную перпендикулярной к направлению движения частицы.

До прохождения частицы через щель ее составляющая импульса p_x имеет значение, равное нулю: p_x = 0 (щель по условию перпендикулярна импульсу), так что D p_x = 0, зато координата x частицы оказывается совершенно неопределенной. В момент прохождения частицы через щель положение меняется. Вместо полной неопределенности x появляется неопределенность D x, но это достигается ценой утраты определенности значения p_x. Действительно, вследствие дифракции имеется некоторая вероятность того, что частица будет двигаться в пределах угла 2 j, где j – угол, соответствующий первому дифракционному максимуму (интенсивность остальных максимумов много меньше, ими мы пренебрегаем). Поэтому появляется неопределенность:

D p_x = p ×sin j.

Краю центрального дифракционного максимума (первому минимуму), получающегося от щели шириной D x, соответствует угол j, для которого

sin j = l /D x,

откуда

D p_x = p ×(l /D x) Þ D x × D p_x = p × l = 2 p ,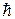

согласующиеся с (*).

Оценим неопределенность координаты и импульса для электрона в электроннолучевой трубке. Пусть след электронного пучка на экране имеет радиус r порядка 10^–3 см, длина l трубки порядка 10 см. Тогда (D p_x / p) ~ 10^–4.

Импульс электрона связан с ускоряющим напряжением U так:

p ²/2 m = eU Þ p = (2 meU)^1/2.

При U ~ 10⁴ В энергия электрона равна 10⁴ (эВ) = 1,6×10^–8 (эрг). Оценим р:

р = (2×0,91×10^–27×1,6×10^–8)^1/2» 5×10^–18 Þ D p_x = 5×10^–18×10^–4 = 5×10^–22.

Согласно (*)

D x» (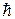 /D p_x) = (1,06×10^–27)/(5×10^–22)» 2×10^–6 см.

Полученный результат свидетельствует о том, что движение электрона в этом случае будет практически неотличимо от движения по траектории.

В классической механике мы при изучении импульса и закона его сохранения рассматривали взаимодействие двух шариков. Поступим так же в квантовой физике.

Рассмотрим покоящуюся частицу массы М, которая распадается в две частицы, разлетающиеся на столь большое расстояние друг от друга, что взаимодействие между ними отсутствует.

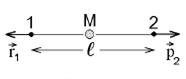Для первой частицы проведем измерение точного значения координаты 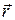₁, а для другой частицы – измерение точного значения импульса ₂. Из закона сохранения импульса следует, что ₁ = – ₂. Тем самым точно определены и ₁, и ₁ первой частицы, что запрещено принципом неопределенности. Поэтому

* Разлетающиеся частицы нельзя рассматривать как независимые, даже если они разлетелись на большое расстояние. Они образуют одну квантовую систему. Квантовая система неделима, не может быть разбита на части, и как целое описывается одной волновой функцией Y. Эту волновую функцию нельзя представить, как произведение волновых функций отдельных частиц: Y ¹ Y₁×Y₂ (волновая функция выражает вероятность, а перемножаются вероятности только независимых событий). Результаты измерений, проводимых над частицами в разных частях одной и той же квантовой системы, зависимы друг от друга. Такая зависимость называется квантовыми корреляциями. Измерение ₂ должно так повлиять на результат измерения 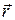₁, что соотношение неопределенностей останется ненарушенным.

В классике мы придерживались принципа близкодействия – все изменения движения должны передаваться от частицы к частице с конечной скоростью, не превышающей скорости света в вакууме с = 3×10⁸ м/с.

В квантовой физике от этого принципа мы отказываемся. Здесь действует принцип дальнодействия – мгновенная передача информации на расстояние l (размер квантовой системы, который может быть сколь угодно велик). Квантовые корреляции означают, что результат измерения в точке 1 влияет на результат одновременного измерения в точке 2.

Date: 2015-06-08; view: 721; Нарушение авторских прав