Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Волновая функция свободной микрочастицы
|
|
Корпускулярные и волновые свойства фотона и микрочастицы аналогичны. Фотону с энергией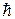 
w, летящему вдоль оси x, можно сопоставить волновую функцию плоской монохроматической волны, распространяющейся вдоль оси x:
E (x) = E 0cos(wt – kx), где k = 2 p / l,
Е – напряженность электрического поля волны – световой вектор.
В комплексном виде: E (x, t) = E 0e– i ( wt – kx ).
Замена частоты и длины волны фотона на частоту и длину волны де Бройля:
w Б = E / 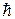; l Б = 2 p 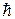/ p
приведет к тому, что мы получим волновую функцию свободной микрочастицы с энергией Е и импульсом р, летящей вдоль оси x:
Y(x, t) = A e– i ( w Б – 2 px / l Б) = A e– i (Et – px)/ ,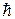
где А – некоторая постоянная.
Для частицы, движущейся в произвольном направлении:
.
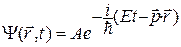То, что волновая функция комплексна – на страшно, так как физический смысл имеет действительная плотность вероятности, то есть, квадрат модуля волновой функции
dP / dV = |Y|2 = Y*Y = | A |2 = const.
Эта вероятность обнаружения частицы одинакова во всех точках пространства. Мы приписали частице определенный импульс и неопределенность ее координаты D x ~ 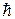/(2×D p) ® ¥ при D р ® 0. кроме того, фазовая скорость плоской волны Y(x, t), которая вычисляется для релятивистской частицы по формуле
V фаз =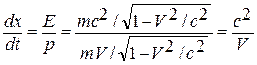 
,
превышает скорость света с, то есть, не сопоставима с истинной скоростью V частицы.
Таким образом, делаем вывод:
* Реальная свободная микрочастица – более сложный объект, чем плоская монохроматическая волна де Бройля.
Будем теперь описывать свободную частицу с импульсом р 0 с помощью волнового пакета, то есть совокупности плоских волн де Бройля со всеми возможными импульсами от p 0 – – D p /2 до p 0 + D p /2 (частица имеет неопределенность импульса D p). Волновая функция пакета получается сложением по принципу квантовой суперпозиции
волновых функций Y(x, t) (см. выше) отдельных волн:
. (*)
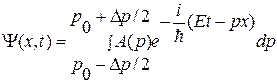Такой пакет имеет конечный размер.
Пусть A (p) = const (пусть также D p мало). Тогда можно разложить энергию микрочастицы в ряд Тейлора:
E (p) = E (p 0) + (¶ E /¶ p)| p = p 0×(p – p 0).
Введем новые обозначения:
a = (¶ E /¶ p)| p = p 0× t – x, x = p – p 0.
Тогда волновая функиця микрочастицы будет иметь вид:
Y(x, t) = C ×e– i / 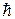(E (p 0) t – p 0 x) 
.
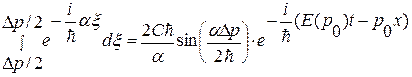Плотность вероятности: |Y(x, t)|2 =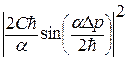 
. Ее зависимость от x в момент времени t изображена на рис.
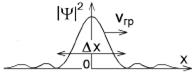|Y(x, t)|2max в точке, где a = 0. Эта точка, то есть место, где вероятность обнаружения частицы максимальна, перемещается вдоль оси x со скоростью
V гр = (¶ x /¶ t)| a =0 = (¶ E /¶ p)| p 0 – групповая скорость волнового пакета, которая определяется для волн де Бройля как V гр =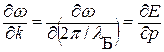 
.
Для свободной микрочастицы E = p 2/2 m, V гр = p 0/ m = V 0 – скорость классической частицы с импульсом р 0.
Размер микрочастицы, то есть ее координаты D x можно сопоставить с шириной центрального пика (см. рис. выше). Его границы соответствуют при t = 0 условию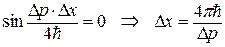 
.
Микрочастицу можно представить как пакет волн де Бройля с волновой функцией (*), который занимает в пространстве конечный объем с размером D x и движется со скоростью классической частицы p 0/ m = V 0 – «облако» плотности вероятности обнаружения частицы |Y|2, перемещающееся вдоль оси x.
! Но: волны де Бройля с разностью импульсов D р имеют разность скоростей D V @ D p / m. Поэтому волновой пакет должен расплываться со временем.
Это аналогично явлению дисперсии электромагнитных волн. Пусть начальный размер электрона D x 0 ~10–16м. Тогда D V @ D p / m = (4 p 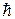)/(m D x 0)и спустя одну секунду он расплывется до размера D x = D x 0 + D V × t ~ (4 p 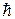)/(m D x 0) × t» 1010 км!
Это произошло от того, что мы предположили, что A (p) = const, а такой пакет будет быстро расплываться. Чему равно A (p)?
Получим общее уравнение, определяющее зависимость Y(x, t) от координат и времени.
Date: 2015-06-08; view: 1027; Нарушение авторских прав