Стационарное уравнение Шредингера

Если частица движется в стационарном поле и ее потенциальная энергия не зависит от времени явно, то уравнение

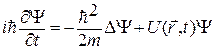
допускает разделение переменных: .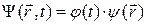

Подставим это разделение в уравнение Шредингера и разделим почленно обе части этого уравнения на произведение j × y:

.

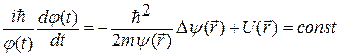Правая и левая части последнего уравнения являются независимыми функциями разных переменных t и r. Они равны между собой только тогда, когда равны некоторой константе. Определим ее. Подставим (*) с соотношения

E = 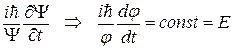Þ

.

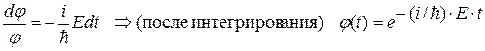Таким образом, в стационарном внешнем поле зависимость волновой функции микрочастицы от времени учитывается экспоненциальным множителем:

.

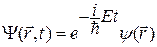Волновая функция 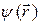, зависящая только от координат, является решением стационарного уравнения Шредингера:

.

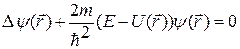При движении частицы вдоль одной оси координат:

.

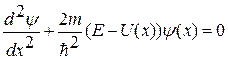* Поле U (r), в котором находится частица, считается известным. Стационарное равнение Шредингера позволяет найти и волновую функцию 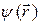частицы в заданном поле, и все разрешенные значения ее полной энергии Е. Для этого при решении дифференциального уравнения Шредингера обязательно надо задать граничные условия для функции 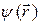или для плотности вероятности обнаружения частицы | y |². И вероятность | y |², и волновая функция y должны меняться плавно, без скачков.

Date: 2015-06-08; view: 479; Нарушение авторских прав