
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Составить уравнение касательной и нормали к кривой в точке
|
|
Решение: Найдем сначала 
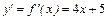 ,
,
подставляя координату 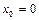 точки
точки 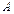 , получаем
, получаем
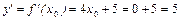 .
.
Подставляя 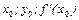 в формулу (2), находим уравнение касательной
в формулу (2), находим уравнение касательной
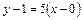 или
или 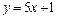 .
.
Подставляя 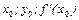 в формулу (3), выводим уравнение нормали
в формулу (3), выводим уравнение нормали
 или
или 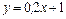 .
.
Тангенс угла, образованного касательной с осью абсцисс, равен 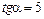 , откуда
, откуда 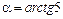 .
.
Ответ: уравнение касательной 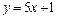 ; нормали
; нормали 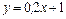 ; угол
; угол 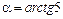 .
.
7. Провести полное исследование функции  и построить ее график.
и построить ее график.
Решение.
1). Область определения функции.
Очевидно, что эта функция определена на всей числовой прямой, кроме точек “  ” и “
” и “ 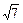 ”, т.к. в этих точках знаменатель равняется нулю и, следовательно, функция не существует, а прямые
”, т.к. в этих точках знаменатель равняется нулю и, следовательно, функция не существует, а прямые  и
и 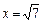 – вертикальные асимптоты.
– вертикальные асимптоты.
2). Поведение функции при стремлении аргумента к бесконечности, существование точек разрыва и проверка наличия наклонных асимптот.
Проверим сначала как ведет себя функция при приближении к бесконечности влево и вправо.
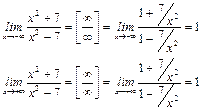
Таким образом, при  функция стремится к 1, т.е.
функция стремится к 1, т.е. 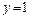 – горизонтальная асимптота.
– горизонтальная асимптота.
В окрестности точек разрыва поведение функции определяется следующим образом:
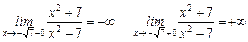
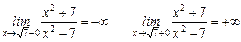
Т.е. при приближении к точкам разрыва слева функция бесконечно убывает, справа – бесконечно возрастает.
Наличие наклонной асимптоты определим, рассмотрев равенство:
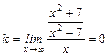 .
.
Наклонных асимптот нет.
3). Точки пересечения с осями координат.
Здесь необходимо рассмотреть две ситуации: найти точку пересечения с осью Ох и с осью Оу. Признаком пересечения с осью Ох является нулевое значение функции, т.е. необходимо решить уравнение:
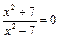
Это уравнение не имеет корней, следовательно, точек пересечения с осью Ох у графика данной функции нет.
Признаком пересечения с осью Оу является значение х = 0. При этом
 ,
,
т.е. 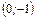 – точка пересечения графика функции с осью Оу.
– точка пересечения графика функции с осью Оу.
4). Определение точек экстремума и промежутков возрастания и убывания.
Для исследования этого вопроса определим первую производную:
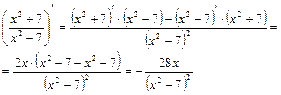 .
.
Приравняем к нулю значение первой производной.
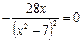 .
.
Дробь равна нулю, когда равен нулю ее числитель, т.е.
 .
.
Определим промежутки возрастания и убывания функции.
Таблица 5
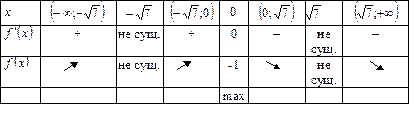
Т.о., функция имеет одну точку экстремума и в двух точках не существует.
Таким образом, функция возрастает на промежутках  и
и 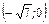 и убывает на промежутках
и убывает на промежутках 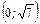 и
и 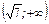 .
.
Как видно из таблицы 5, 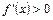 при
при 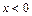 и
и 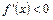 при
при 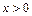 , т.е. при
, т.е. при 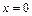 функция имеет максимум.
функция имеет максимум.
5). Точки перегиба и участки выпуклости и вогнутости.
Эта характеристика поведения функции определяется с помощью второй производной. Определим сначала наличие точек перегиба. Вторая производная функции равна
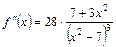 .
.
Таблица 6
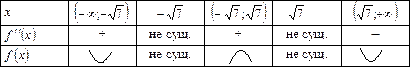
При 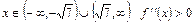 и функция вогнута; при
и функция вогнута; при 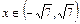
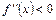 и функция выпуклая.
и функция выпуклая.
6). Построение графика функции.
Используя в пунктах найденные величины, построим схематически график функции:
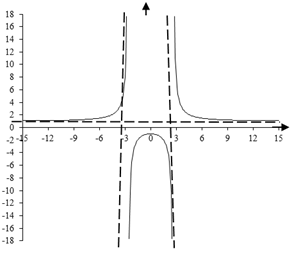
Рис.5
8. Дана функция 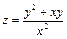 . Показать, что
. Показать, что 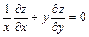 .
.
Решение. Вычислим частные производные:
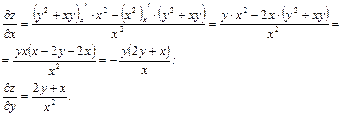
Тогда
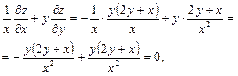
что и требовалось доказать.
Date: 2015-06-08; view: 989; Нарушение авторских прав