Функции нескольких переменных и их дифференцирование

Определение: Переменная z называется функцией переменных x è y, если каждой паре значений x и y поставлено в соответствие определенное значение z.

Функциональная зависимость z от x и y записывается в виде z=f(x,y). Аналогичным образом определяются функции трех и более переменных.

Функции двух переменных допускают геометрическую интерпретацию. Графиком функции z=f(x,y), определенной в области G, называется множество точек (x,y,z) пространства, у которых (x,y) принадлежат G и z=f(x,y). В наиболее простых случаях такой график представляет собой поверхность (рис. 3).

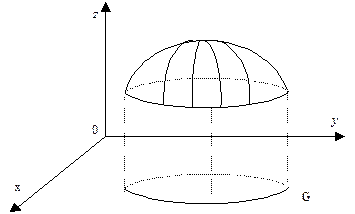
Рис. 3

Частной производной функции нескольких переменных по какой-либо переменной в рассматриваемой точке называется обычная производная по этой переменной. При этом другие переменные считаются фиксированными (постоянными).

Для функции z=f(x,y) в точке A(x₀;y₀) частные производные определяются следующим образом:

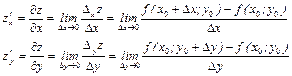
если эти пределы существуют.

Из определения частных производных следует, что правила их вычисления остаются такими же, как и для функции одной переменной, только необходимо помнить, по какой переменной ищется производная.

Частными производными второго порядка называют частные производные, взятые от частных производных первого порядка.

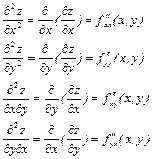
Частные переменные 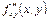и 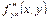называются смешанными. В теории доказывается, что в тех точках, где производные непрерывны, смешанные производные совпадают.

Найдем частные производные второго порядка функции 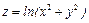. Сначала вычислим частные производные первого порядка

.

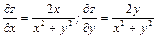Тогда

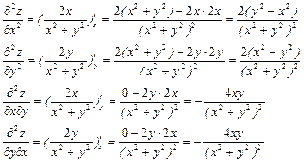
Видно, что смешанные производные равны

.

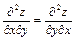Пример 3. Дана функция .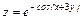

Показать, что 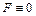; где .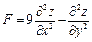

Решение: вычислим сначала 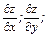а затем и .

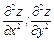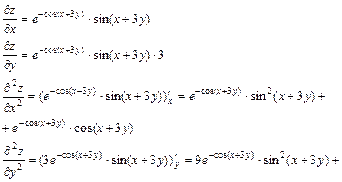
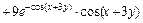
Тогда

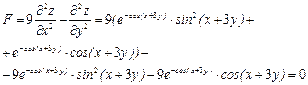
Ответ: 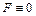, что и требовалось доказать.

Date: 2015-06-08; view: 726; Нарушение авторских прав