Замена и консолидация платежа

Пример 1. Согласно новому финансовому соглашению платеж 80 000 руб. со сроком уплаты 6 месяцев заменяется платежом со сроком уплаты 3 месяца. Найдите величину нового платежа, если используется простая процентная ставка 20 % годовых.

Решение. Пусть P₁ = 80 000 руб., r = 0,4. Считая, что год содержит 360 дней и каждый месяц - 30 дней, полагаем n₁ = 0,5 года

Полагая n₀ = 0,25 года и учитывая, что n₀ < n₁, по формуле получим:

P₀ = 80 / (1 + (0,5 – 0,25) • 0,2) = 76 190 руб.

Этот же результат можно получить, и не пользуясь формулой, а составив для данной конкретной ситуации уравнение эквивалентности, руководствуясь принципом финансовой эквивалентности. В соответствии с этим принципом величина платежа Ро должна быть такой, что, получив через 3 месяца (nо = 0,25 года) P₀ и инвестировав эту сумму под простую процентную ставку r = 0,2, кредитор через время n₁ – n₀ мог бы получить сумму P₁ = 80 тыс. руб. Таким образом, получим уравнение: P₁ = P₀ • (1 + (n₁ – n₀) • r), в котором неизвестной величиной будет P₀

Обратим внимание на следующий факт. Если не применять принцип финансовой эквивалентности, а просто воспользоваться равенством приведенных стоимостей (на начальный момент времени) этих платежей, т.е. соотношением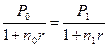

то платеж P₀ будет равен:

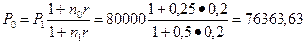
Эта сумма больше, чем 76 180 руб. Инвестировав 76363 руб. под 20% годовых, кредитор через 3 месяца (n₁ – n₀ = 0,2 года) получил бы

76 363 • (1 + 0,25 • 0,2) = 80 181,81 руб.

т.е. на 181,81 руб. больше, чем было предусмотрено первым финансовым соглашением.

Пример 2. Найдите величину нового срока, если платеж в 20 000 руб. с уплатой через 250 дней предполагается заменить платежом в 18 000 руб. Используется простая процентная ставка 17,5 % годовых, и расчетное число дней в году равно 360.

Решение. Очевидно, что так как 18 000 руб. меньше 20 000 руб., то новый срок по должен быть меньше 250 дней. Полагая P₁ = 20 000 руб., n1 = 250/360 года, P₀ = 18 000 руб., r = 0,175, по формуле для случая P₀ < P₁ получим:

n₀ = 250/360 – (20/18 – 1)/0,175 = 0,675 года, или n₀ ≈ 243 дней.

Пример 3. Платежи в 6, 4 и 10 тыс. руб. должны быть погашены соответственно через 90, 165 и 270 дней. Кредитор и должник согласились заменить три платежа одним через 120 дней. Найдите величину консолидированного платежа, если используется простая процентная ставка 19 % годовых и в расчет принимаются обыкновенные проценты.

Решение. При решении задач такого типа пользуются уравнением эквивалентности, согласно которому сумма заменяемых платежей, приведенных к одному моменту времени, приравнивается к сумме платежей по новому соглашению, приведенных к той же дате. Причем приведение осуществляется путем дисконтирования к более ранней дате или путем наращения величины соответст­вующего платежа, если эта дата относится к будущему.

В данном случае платежи в 6, 4 и 10 тыс. руб. заменяются единым платежом Pо, величину которого обычно определяют путем приведения всех платежей к дате погашения платежа P₀.

Так как срок погашения платежа в 6 тыс. руб. меньше 120 дней, то процесс приведения для этого платежа будет осуществляться в виде процесса наращения в течение 30 дней (120 - 90) по простой процентной ставке 19 % годовых.

Так как срок погашения платежа в 4 тыс. руб. больше 120 дней, то процесс приведения для этого платежа будет осуществляться в виде процесса дисконтирования по простой процентной ставке 19 % годовых за 45 дней (165 - 120). По той же причине сумма 10 тыс. руб. дисконтируется за 150 дней (270 - 120).

Складывая приведенные суммы платежей, получим величину консолидированного платежа P₀:

P₀ = 6/(1+30 • 0,19/360) + 4/(1+45 • 0,19/360) + 10/(1 + 150 • 0,19/360) = 19 268,58 руб.

Если бы за дату приведения выбрали, например, время выплаты платежа в 6 тыс. руб., то, рассуждая, как и выше, получили бы такое уравнение:

Р₀ /(1+30 • 0,19/360) = 6 + 4/(1 + 75 • 0,19/360) + 10/(1 + 270 • 0,19/360)

Откуда Р₀ =19 683 руб.

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

1. Капитоненко В.В. Задачи и тесты по финансовой математике: учеб. пособие – М.: Финансы и статистика, 2007. – 256 с.

2. Бочаров П.П., Касимов Ю.Ф. Финансовая математика: Учебник. – 2-е изд. – М.: ФИЗМАТЛИТ, 2005. – 576 с.

3. Батракова Л.Г. Финансовые расчеты в коммерческих сделках. – М.: Лотос, 2004.

4. Крничановский К.В. Математика финансового менеджмента: учебное пособие. – М.: Дело и сервис, 2006.

5. Ковалев В.В., Уланов В.А. Курс финансовых вычислений. – М.: Финансы и статистика, 2006.

6. Мелкумов Я.С. Теоретическое и практическое пособие по финансовым вычислениям. – М.: ИНФРА-М, 2004

7. Смирнова Е.Ю. Техника финансовых вычислений на Excel: Учеб. Пособие. – СПб.: ОЦЭиМ, 2006.

8. Кочович Е. Финансовая математика с задачами и решениями. – М.: Финансы и статистика, 2004.

9. Кочович Е. Финансовая математика: теория и практика финансово-банковских расчетов. – М.: Финансы и статистика, 2005.

10. Четыркин Е.М. Финансовая математика. 7-е изд., испр. – М.: Дело, 2007.

11. Ковалев В.В. Управление активами фирмы: учеб.-практ. Пособие. –М.: Проспект, 2007.

Date: 2015-06-08; view: 2910; Нарушение авторских прав