Влияние на состояние труб концентраторов напряжений

Любые дефекты, связанные с нарушением бездефектной формы конструкции трубы, являются местами концентрации напряже­ний. Попытки исследовать вопрос о концентрации напряжения в дефектных местах труб предпринимались неоднократно, од­нако они проводились экспериментальным путем. Кроме под­тверждения факта концентрации напряжений такие экспери­менты ничего существенного не дали. Поэтому представляет исключительный интерес найти такое теоретическое решение, которое позволило бы количественно оценить распределение на­пряжений в зоне дефекта. Решение может быть получено с помощью численного метода конечных элементов. Мы приведем здесь лишь идею метода, а также основные результаты и раз­работки использования метода конечных элементов при расчете напряженного состояния труб с дефектами. Суть метода заклю­чается в том, что рассматриваемая упругая среда, например стенка трубы, разбивается на конечное число элементов. В слу­чае плоской задачи этими элементами могут быть треугольники, а в случае пространственной — треугольные призмы или тетра­эдры. Все элементы связаны между собой конечным числом уз­ловых связей, что сохраняет упругие свойства среды и напря­женно-деформированное ее состояние, характерное для данного упругого тела. Внутри каждого элемента задают некоторые функции формы, которые позволяют определить перемещения внутри элементов по перемещениям в узлах, являющихся мес­тами стыков конечных элементов. За координатные принима­ются функции, тождественно равные нулю во всех элементах, кроме одного, внутри которого они совпадают с функциями формы. Узловые перемещения в данном случае являются неиз­вестными коэффициентами. Далее записывается функционал полной энергии для всех элементов и находится его минимум. Полученная таким образом система алгебраических уравнений решается с помощью ЭВМ и определяются искомые перемеще­ния и напряжения. Кратко поясним суть метода конечных эле­ментов в применении к определению напряжений и перемеще­ний в дефектных участках труб. Наиболее характерные места дефектов — продольные (заводские) и кольцевые (трассовые) сварные швы (они имеются на всех трубах магистрального тру­бопровода), а также различного рода трещины, царапины и т. п. Все эти дефекты можно рассматривать в осесимметричном либо плоском напряженном состоянии.

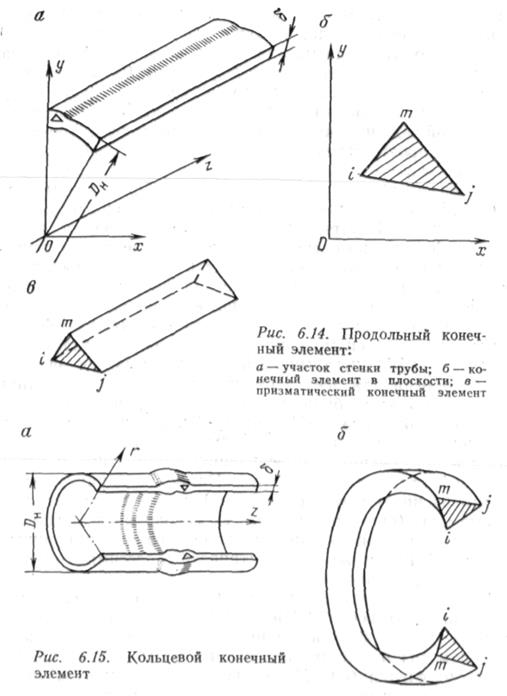
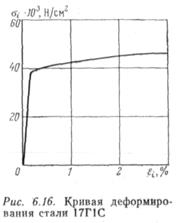
На рис. 6.14 изображены часть трубы с продольным швом и один призматический конечный элемент в продольном свар­ном шве. На рис. 6.15 показаны часть трубы с кольцевым свар­ным швом (а) и кольцевой конечный элемент треугольного по­перечного сечения (б). Метод конечных элементов позволяет учесть упругое и упругопластичное деформированное состояние, а программа, разработанная для ЭВМ, — решить многие за­дачи, связанные г определением напряженно-деформированного состояния в зоне дефекта.

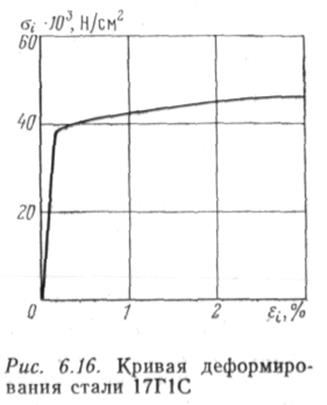
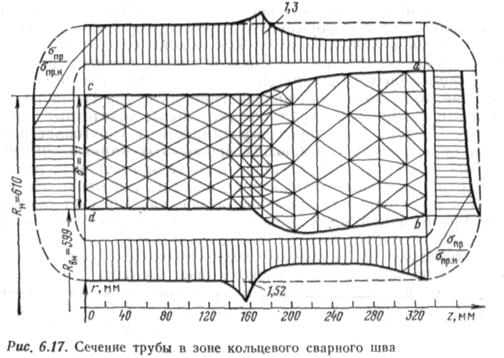
Рассмотрим результаты некоторых расчетов. Осесимметричное напряженно-деформированное состояние в трубах исследо­валось в области кольцевого сварного шва для труб из стали 17Г1С; кривая деформирования изображена на рис. 6.16. На рис. 6.17 показано сечение трубы со сварным швом, в котором определялось напряженно-деформированное состояние. Размеры рассматриваемой области: D_H=1220 мм, 6=11 мм, L = 63,5 мм. Этот участок был разбит на 294 элемента со 178 узлами. Таким образом, задача сводилась к решению 356 линейных

алгебраи­ческих уравнений. В узлах, расположенных на оси симметрии сварного шва ab и на линии cd, были заданы граничные усло­вия, запрещающие перемещения в направлении оси z. В узлах, расположенных по внутреннему контуру трубы, задавались со­средоточенные силы от внутреннего давления. Вначале исследо­валось упругое напряженное состояние. Из условия e_z = 0 сле­дует, что при нагружении трубы внутренним давлением в ней возникают продольные напряжения а_пр=цо„_ц. Как видно из рис. 6.17, в области, удаленной от сварного шва, это соотноше­ние выполняется, В районе шва условие e_z = 0 не выполняется, так как существенна объемность напряженно-деформированного состояния. Для кольцевого шва наиболее существенна концен­трация продольных напряжений. Для рассчитанного реального Сварного шва коэффициент концентрации продольных напря­жений в упругой области составил 1,52 на внутреннем контуре и 1,3 на внешнем контуре трубы. Следует отметить, что эти зна­чения справедливы для любой продольной нагрузки за исклю­чением той, которая вызывается объемными силами. Для тру­бопроводов такими нагрузками являются усилия, возникающие от температурных перепадов.

В качестве примера влияния температурных напряжений рассмотрим результаты расчета напряженно-деформированного состояния в районе сварного шва при действии внутреннего дав­ления и температуры. В расчете принято Л/= 75 °С. Основной особенностью температурного нагружения области сварного шва

является то, что в продольном на­правлении существенным стано­вится изгиб. Напряжения изгиба возникают из-за несимметрии про­дольного сечения сварного шва от­носительно средней линии стенки трубы. Этим объясняется сущест­венное отличие результатов расчета с учетом температуры, приведенных на рис. 6.18, от результатов, при­веденных на рис. 6.17.

На рис. 6.18 сплошными лини­ями показано упругое распределе­ние продольных напряжений, а пунктирными — упругопластичное. Расчеты выполнены при давлениях

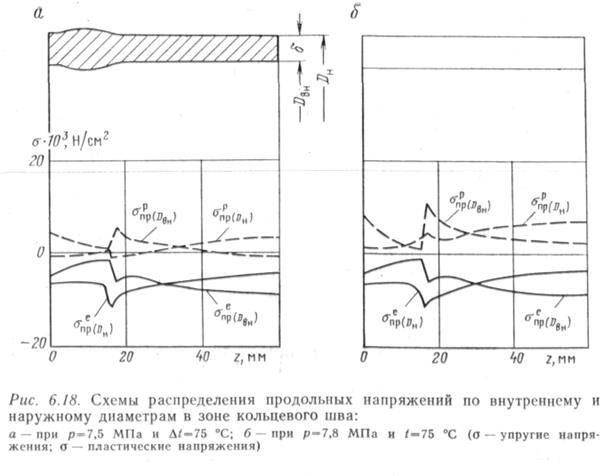
р = 7,5 МПа и р = 7,8 МПа, вызывающих кольцевые напряжения, равные соответственно 0_кц=40,8-10³ Н/см²; а_Кц = 42,8-10³ Н/см².

Особенностью деформирования трубопровода является то, что из условия в₂ = 0, которое выполняется и в упругопластичной области, следует соотношение е/ = —е/, где е_г^р — остаточ­ные пластические деформации в направлении z, а е/— упругие деформации в направлении г. Так как на основании теоремы о разгрузке остаточные напряжения равны разности напряже­ний, полученных при упругопластичном и упругом их распре­делении, то в продольном направлении после упругопластичного деформирования возникают положительные остаточные напря­жения. Поэтому, если труба деформируется в упругопластичной области и области сжимающих продольных напряжений, выз­ванных температурным расширением, то при анализе прочно­сти труб продольные напряжения можно не учитывать. На этот факт следует обратить внимание особое, так как учет сжимаю­щих продольных усилий приводит к существенному увеличению толщины стенки трубы.

Рассмотрим далее плоское деформированное состояние труб на примере продольного сварного шва. Область продольного сварочного шва была разбита на конечные элементы. Коорди­наты узлов задавались для участка трубы, изображенного на рис. 6.14. В данной задаче решалось 356 линейных алгебраиче­ских уравнений. Результаты расчета в упругой и

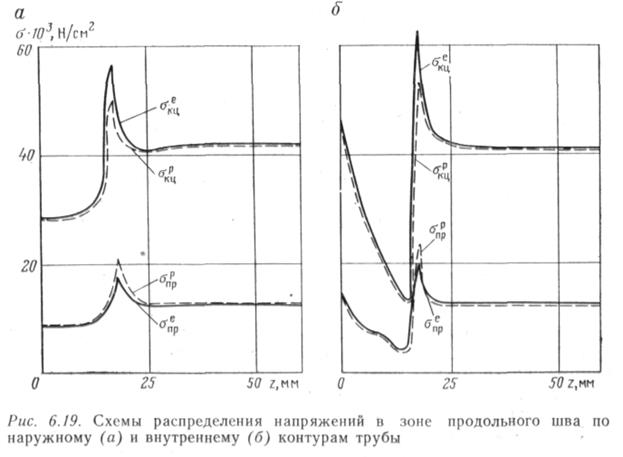
упругопластичной областях представлены на рис. 6.19. Наибольшие напря­жения возникают на внутреннем контуре трубы, причем упру­гий коэффициент концентрации напряжений &_е=1,49, а упруго-пластичной— k_p=\,28. На наружном контуре трубы упругий коэффициент концентрации напряжений составляет й_е=1,34, а упругопластичный — &_р=1,19. В ряде случаев, зная k_p и кри­вую деформирования, можно найти k_c, используя приближенное соотношение k_p= I -f (k_e — 1) E*jE, где Е* — секущий модуль кри­вой деформирования.

По предложенной методике можно исследовать также напря­женно-деформированное состояние в зоне забоин, надрезов, трещин.

Date: 2015-06-07; view: 1453; Нарушение авторских прав