Вероятностный анализ предельного состояния трубопровода

Как было отмечено, в случае радиального напряженного со­стояния р_пр следует определять по формуле (6.9). Тогда функ­ция неразрушимости принимает вид

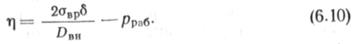
ые параметры, входящие в (6.10), — случайные ве­личины, которые можно охарактеризовать функциями распре­деления, полученными статистическим путем или на основании теоретических соображений. Функция т| нелинейно зависит от перечисленных параметров. Однако, так как отклонения вели­чин а_вр, dbh, б и рраб невелики по сравнению с их математиче­скими ожиданиями, то функция т] может быть заменена линей­ной зависимостью путем разложения в ряд Тейлора в окрестно­сти математических ожиданий случайных величин. В результате т] принимает вид

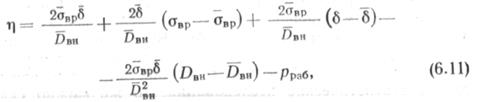
где а_вр, б~ О„„ — математические ожидания соответствующих ве­личин.

В формуле (6.11) т) является линейной функцией определяю­щих параметров и ее можно представить как

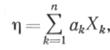
где uk — постоянный коэффициент; Xk — случайная величина; п — число случайных параметров.

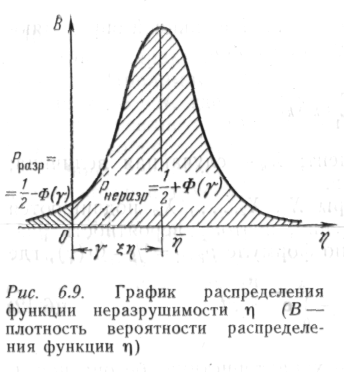
Все определяющие параметры Х\, Хч, • • •, Х„ подчиняются нормальному закону распределения, поэтому вероятность раз­рушения трубопровода найдем по формуле р_Разр='/2— Q>(f), где

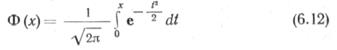
-функция Лапласа; у= 1/ю_ч— характеристика безопасности, введенная А. Р. Ржаницыным, которая представляет число стан­дартов, укладывающихся на отрезке 0— г\ (рис. 6.9);

- коэффициент изменчивости функции неразрушения;

- математическое ожидание функции неразрушения;

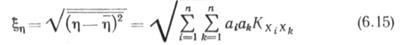
— среднее квадратическое отклонение функции ц;

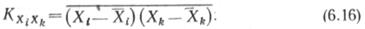
Учитывая формулы (6.13) — (6.16), характеристику у пред­ставим в виде

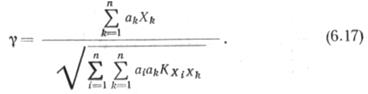
Из величин, входящих в (6.11), корреляционная связь может существовать между толщиной стенки труб, пределом прочно­сти материала и диаметром труб. Для исследования этого вопроса были проанализированы

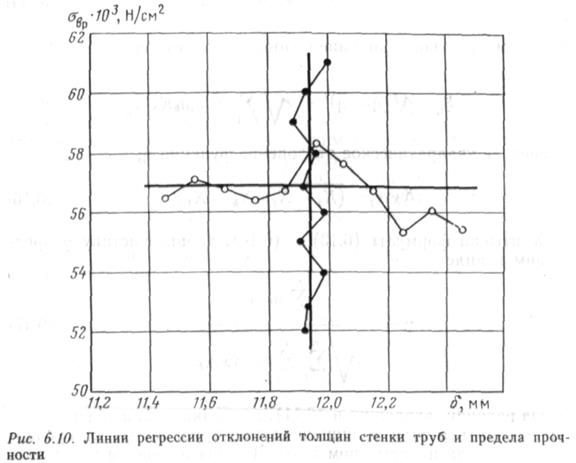
результаты испытаний образцов, вырезанных из труб. По
данным распределения толщин стенок труб и пределов
прочности образцов определены условные средние их
значения и построены линии
регрессии (рис. 6.10, жирные
линии). Так как эти прямые
взаимно перпендикулярны, то
можно сказать, что /Са_врб = 0.
Распределение диаметров труб в основном зависит от параметров технологического процесса производ-ства и не связано с распределением толщин и свойств материала. Поэтому величины, входящие в (6.10), не коррелированы между собой.

Остановимся далее на распределении пределов прочности материала труб и на факторах, оказывающих на них влияние. Были обработаны данные лабораторных испытаний около 70000 образцов, вырезанных из труб различных диаметров и толщин стенок б. Материал труб — сталь 17Г1С, размеры образцов

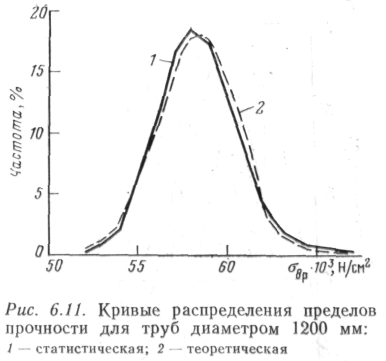
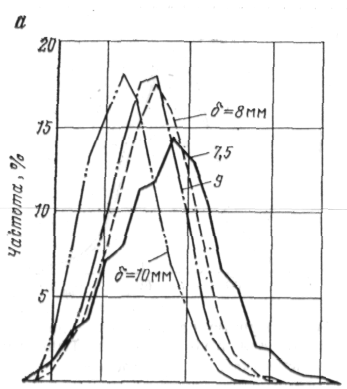
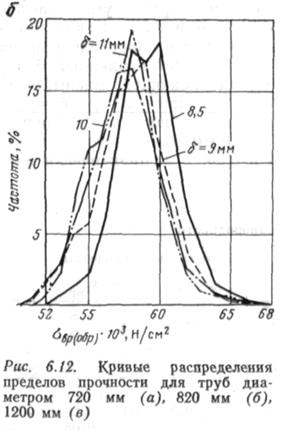
ЗООхЗОхб мм. Из при­веденных для примера на рис. 6.11 и 6.12 кривых распределения ог„р для труб диаметром 820 и 1220 мм видно, что, не­смотря на малый объем образцов, совершенно очевидно отклонение кри­вых для больших толщин стенок влево, что свиде­тельствует о влиянии на предел прочности труб масштаб-ного фактора. Выполненная математи­ческая обработка позво­ляет утверждать, что предел прочности сгвр с увеличением объема образца уменьшается. Это дает основание сказать также, что и фактическая проч­ность трубы должна быть ниже прочности, определенной на образцах малого объема. Поскольку это установленный факт, то необходимо найти зависимость, оценивающую масштабный фактор, например, с помощью введения масштабного коэффи­циента. Выполненные вычисления масштабного коэффициента для труб диаметром 720, 820 и 1220 мм дают соответственно следующие значения v: 0,84; 0,84 и 0,85, т. е. практически оди­наковые значения.

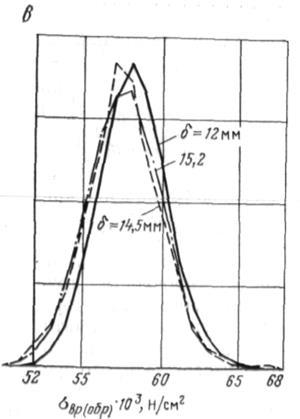
Другим объективным ка­чеством, определяющим раз­брос значений о_вр, является неоднородность свойств ма­териала, оцениваемого так называемым коэффициен­том однородности. Рассмот­рим статистическое обосно­вание этого коэффициента. Представим его в виде

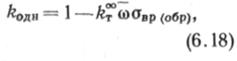
где /г_т°° — односторонний то­лерантный предел для гене­ральной совокупности (п = = о°), определяющий, ско­лько средних квадратиче-ских отклонений необхо­димо отнять от математического ожидания предела прочности трубы, чтобы вероятность разрушения составила 1-Я (Г) [Р(Т) —вероятность неразру­шения]. Толерантный предел fe_T°° получают из зависимости Фо(*т°°)=Р(7')-0₎5.

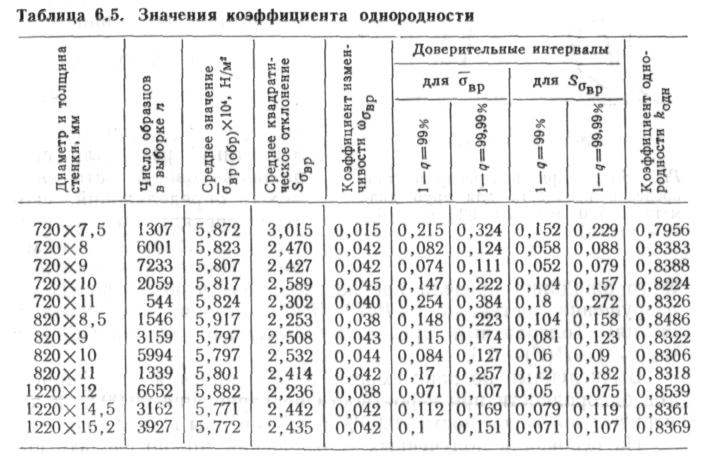
Вычисленные по зависимости (6.18) значения коэффициен­тов однородности при вероятности неразрушения 99,99 % и до­верительной вероятности 99,99% представлены в табл. 6.5.

На основании полученных соотношений можно сделать вывод, что для обеспечения прочности труб с заданной вероят­ностью неразрушения напряжения в их стенке не должны пре­вышать

Например, для трубы 1220Х 14,5 мм с вероятностью нераз­рушения Р(Т) = 99,99% предельные кольцевые напряжения не должны превышать значения а_пр=0,8361-0,85-5,771 • 10^=4,IX ХЮ³ Н/см². Это на 28 % меньше, чем среднее значение сг_вр(обр), полученное при испытании образцов.

Выполненное теоретическое обоснование коэффициентов од­нородности и масштабного имеет важное значение для опреде­ления действительной несущей способности труб с соответ­ствующей мерой неразрушимости или надежности.

Учитывая изложенное, а также принимая во внимание за­висимость (6.17) и обозначая условный коэффициент запаса не­сущей способности трубы

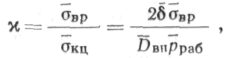
где Ок_Ц, б, D_Bn, р_Ряб — математическое ожидание соответственно кольцевых напряжений, толщины стенки, внутреннего диаметра и рабочего давления, получаем для характеристики безопасно­сти выражение

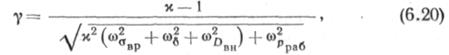
в котором (о — коэффициенты изменчивости величин, обозна­ченных индексом (со_0вр, со_б, Ио_вн,»_Лраб).

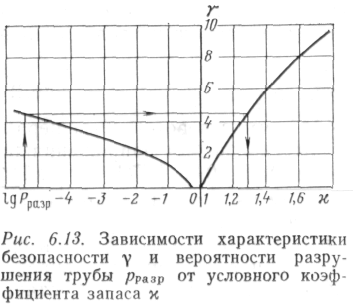
В зависимости от коэффициента запаса к характеристика безопасности принимает различные значения. Чем меньше ко­эффициент запаса, тем больше вероятность разрушения. Для примера в табл. 6.6 приведены значения расчетных величин, входящих в формулу (6.20), полученные для труб из стали 17Г1С размером 1220X12 мм, а на рис. 6.13 изображена

зависимость характеристики безопасности у и вероятно­сти разрушения трубы ррззр от коэффициентов за­паса х.

Если рассчитать меру надежности для бездефект­ного трубопровода 1220Х Х12 мм из стали 17Г1С при 0_Кц = 0,650_Вр, то коэф­фициент запаса оказыва­ется равным 1,53, характе­ристика безопасности у = = 9,77, а вероятность раз­рушения 0_ра3р=1,93-10~¹³. Соответственно мера надежности трубопровода будет Р(Т) = = 0,99999999 и т. д. Оказывается, что бездефектный трубопро­вод имеет очень высокий уровень (меру) надежности. Чем же объяснить, что разрушения трубопроводов довольно часты? Прежде всего наличием большого числа разного рода дефек­тов. Поэтому столь высокий коэффициент запаса несущей способности является средством компенсации самых разнооб­разных дефектов (строительных, металлургических и т. д.) тол­щиной стенки труб, т. е. совершенно неоправданным перерас­ходом металла труб.

Методы количественной оценки влияния различных дефек­тов на уменьшение несущей способности труб при использова­нии средств, выявляющих опасные дефекты до сдачи трубопро­вода в эксплуатацию, дают возможность снизить коэффициент запаса до 1,1—1,2 и резко сократить расход металла.

Рассмотренные в данном параграфе задачи позволяют на ос­нове вероятностного подхода количественно оценить меру на­дежности трубопровода, не имеющего дефектов, вызывающих образование местных разрушений, переходящих в разрушения общего характера (разрыв труб, протяженные разрушения).

Date: 2015-06-07; view: 1322; Нарушение авторских прав