
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Оптимальное профилирование
|
|
Под оптимальным будем понимать профиль, при котором требуются минимальные затраты на обеспечение высотного положения трубопровода и выполняются необходимые условия по надежности, зависящие от этого положения. К ним относятся обеспечение продольной устойчивости, защита от механических повреждений, обеспечение необходимой тепловой защиты и т. п. Перечисленные условия обеспечиваются необходимой глубиной заложения Л3, пригрузкой или закреплением труб анкерами, установкой кривых труб малого радиуса, упругим искривлением трубопровода. Перед началом профилирования должны быть определены и четко зафиксированы: минимально допустимая глубина заложения труб /i3min, наибольшая глубина заложения Лятят, минимальный радиус упругого искривления 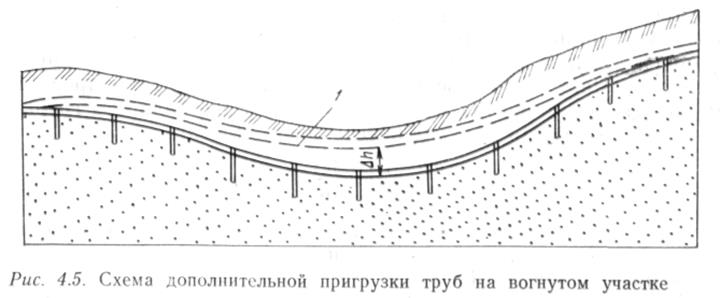
трубопровода /?min, радиус кривизны поворотов из кривых труб /?„р.
Рассмотрим сначала случай профилирования только при упругом искривлении труб. При условии выполнения перечисленных требований должен быть получен минимум затрат на земляные, изоляционно-укладочные работы и работы по пригрузке труб. Кроме того, должны быть обеспечены прилегание труб к дну траншеи и прочность трубопровода. Условие прилегания труб к грунту обеспечивается, если

где ф(л:)—упругая реакция грунта основания; q(x) —распределенная нагрузка от массы труб, пригрузки и удерживающей силы анкерных креплений.
Реакция грунта может возникнуть только в случае ф(;с)>0; именно это условие и определяет прилегание труб к дну траншеи. С учетом этого из уравнения (4.9) получим условие прилегания в виде

Поясним значение q(x). Если прилегание труб происходит только за счет силы тяжести, то q(x)=q = consi и равно силе тяжести единицы длины труб. Если прилегание обеспечивается пригрузкой бетонными и иными утяжеляющими грузами, то

где qrp(x) —распределенная на единицу длины трубы сила тяжести отдельных грузов.
Анкерное крепление при профилировании в качестве нагрузки учитывается только в том случае, если с помощью анкеров «дожимают» трубопровод на вогнутом участке рельефа, например, как показано на рис. 4.5. Если бы трубопровод был уложен без утяжеления или анкеров,
то он бы занял положение /. С помощью анкеров трубопровод можно «дожать» до дна траншеи. Однако на практике такой способ пригрузки не применяется. Часто для обеспечения устойчивости трубопровода на обводненных грунтах используют в качестве балласта грузы. Прочность труб при укладке обеспечивается, если

где /?min определяется по формуле (4.2) или задается, исходя из каких-либо иных соображений, например, из условия обеспечения продольной устойчивости.
Наконец, условие собственно оптимизации профиля можно записать в виде функции затрат на земляные работы и пригрузку труб:
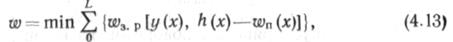
где ш3. р — затраты на выполнение земляных работ в сечении х; у(х), h(x) —соответственно отметки дна траншеи и поверхности грунта в том же сечении; wn(x) —распределенная пригрузка от веса грузов в сечении х.
Задача (4.13) может быть решена различными методами, в частности, с использованием динамического программирования или идеи оптимального управления при наложении ограничений на поведение функции у(х) во всех точках вдоль участка рассматриваемой длины L. Это ограничение имеет следующий вид. В местах предусмотренных разрывов трубы, например в местах установки отсекающей арматуры (кранов, задвижек),
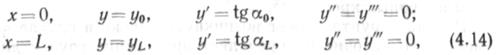
где «о и а/, — углы наклона оси трубопровода к горизонту в сечениях х = 0 и x — L. Кроме того, во всех сечениях *>0 должны выполняться условия (4.12) и (4.13).
При использовании динамического программирования при профилировании задача решается в сеточной постановке как многошаговый процесс. Недостаток подхода — необходимость представления области поиска оптимального профиля в виде сетки. При этом упругая линия трубопровода представляется в виде ломаной линии, состоящей из отдельных прямых участков. Чтобы приблизить очертание этой ломаной к реальной упругой линии трубопровода, нужно брать сетку с очень малым шагом по вертикали Л/i и достаточно большим — по горизонтали Лх. На рис. 4.6 показаны сетка с упругой линией (пунктир) и ее изображение в виде ломаной линии. Увеличение числа элементов ДЛ существенно усложняет процесс расчета профиля на ЭВМ.

Для решения задачи профилирования, рассматриваемой как отыскание наилучшего положения линии трубопровода в ограниченной высотными отметками полосе, можно применить теорию оптимального управления процессом. Необходимо найти минимум функции затрат, обусловленных высотным положением трубопровода. Математически сформулированная эта практически важная задача относится к задачам вариационного исчисления. Что понимается в задаче оптимального профилирования под оптимальным управлением процессом, проиллюстрируем следующим образом. Пусть мы имеем функционал затрат на профилирование в виде
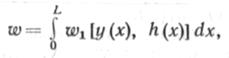
где Ш| — затраты на профилирование единицы длины трубопровода в сечении х; у(х) и h(x) —соответственно высотные отметки дна траншеи и поверхности грунта. Допустим далее, что заданы высота полосы профилирования h(x) — y(x)=A, длина участка L, в пределах которого осуществляется ход управляемого процесса, а также ряд ограничений в виде условий (4.12), (4.13) и (4.14). Необходимо найти такое управление w\ при перечисленных ограничениях, при котором функционал (4.15) достигнет минимума.
Оптимальный профиль будем определять от приближенно заданного начального положения трубопровода, описываемого начальной функцией «/0 = /о(*). В качестве такого начального положения можно принять линию, следующую параллельно линии естественного рельефа местности на глубине Ля. На рис. 4.7 изображены обе эти линии (1,2} и полоса /1В, в пределах которой возможно варьирование линии трубопровода. Если предусматривается чисто подземная схема прокладки, то положение линии трубопровода, изображенное на рис. 4.7, будет предельным по минимуму глубины заложения Лт. Естественно, что функционал (4.15) при таком положении трубопровода на участке OL достигает минимума. Но не во
|
всех сечениях будут выполняться Ограничительные условия (4.10) и (4.12). В зависимости от жесткости труб EI их положение в соответствии с этими условиями должно быть иным. На рисунке эти удовлетворяющие условиям (4.10) и (4.12) положения показаны пунктиоом. Однако затраты w\ для них будут большими, чем для линии /. Задача заключается в том, чтобы, управляя положением упругой линии трубопровода от начального (линия 2) в допустимых по условиям (4.10) и (4.12) пределах, найти положение, в котором функционал (4-15) достигает минимума. Для решения задачи нужно иметь в каждой точке х значение w\. Затраты на профилирование Wi состоят из двух основных составляющих — стоимости земляных работ и стоимости кривых вставок: ш = = о>3.р + а>кр. Величина wa. p зависит от поперечного сечения траншеи, т. е. w3. p = f(w), где со — площадь сечения траншеи, которую можно выразить через ее основные параметры — ширину дна Ь, заложение откосов m и глубину hr. Соответственно Доз. р можно представить в виде функции w3.P = f(m, b, hT). Параметр /it, кроме того, определяет и измененное по сравнению с начальным положение упругой линии трубопровода в точке х, поскольку у(х) = у0(х) —/1Т (х).
Рассмотрим далее систему обыкновенных дифференциальных уравнений, описывающих упругую линию трубопровода:
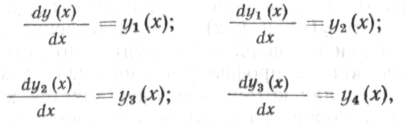
где у(х) —уравнение упругой линии; у\, у2 и yz — соответственно первая, вторая и третья производные от у(х). Управляющей функцией в рассматриваемом случае является функция стоимости земляных работ и установки гнутых кривых вставок малого радиуса w^x). На управляющую функцию Ш] (х) также накладывается ограничение, определяемое следующим образом. Минимум w\ будет определяться только стоимостью земляных работ при устройстве траншеи прямолинейного профиля минимально допустимой глубины; наибольшее значение w\ будет определяться стоимостью разработки траншеи трапецеидального профиля максимально допустимой по условиям строительства или по иным соображениям глубины в пределах участка расчетной длины L плюс установка кривой вставки из гнутых труб. Эти значения w\ определяются предварительно; кроме того, должна быть установлена зависимость w\
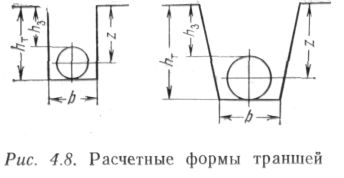
от глубины заложения труб. Так, при профилях траншеи, изображенных на рис. 4.8, стоимость земляных работ на единицу длины траншеи
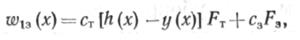
где ст — стоимость устройства единицы объема траншеи (1 м3); с3 — стоимость засыпки единицы объема траншеи после укладки труб; /ч — площадь поперечного сечения траншеи,
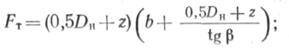
|
| F3 — площадь обратной засыпки. |
Раздел III
Date: 2015-06-07; view: 1266; Нарушение авторских прав