Неравенство Клаузиуса

Итак, мы получили новое и достаточно общее выражение для КПД обратимой тепловой машины (14-10). В то же время начальное определение КПД (14-4) остается в силе, и с его помощью можно оценивать КПД любой (в частности, необратимой) машины. Сравнивая эти два выражения, можно записать (на основании второй теоремы Карно):

,

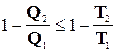или 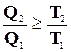. (15-1)

В свою очередь, из выражения (15-1) следует:

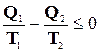. (15-2)

Величины Q₁ и Q ₂, входящие в последнее неравенство, характеризуют количества теплоты, которые получает рабочее тело от нагревателя (Q₁) при постоянной температуре Т₁ и отдает холодильнику (Q₂) при постоянной температуре Т₂. Если свойства нагревателя и холодильника таковы, что в процессе теплообмена с рабочим телом их температуры меняются, то каждый из двух ранее рассматриваемых
квазиравновесных процессов может быть разбит на ряд элементарных процессов, настолько малых, чтобы передачу в ходе каждого из них элементарного количества теплоты dQ_i можно было бы считать происходящим при постоянной температуре Т_i. В этом случае в неравенство (15-2) войдет сумма всех элементарных процессов:

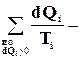
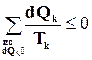(15-2а)

Однако в общем случае, когда рабочее тело может обмениваться с различными нагревателями и холодильниками (т.е. с любыми другими телами), это неравенство

удобно формализовать, приписав всем dQ_i алгебраический смысл: элементарная теплота положительна, если она сообщается рабочему телу, и отрицательна, если эту теплоту отбирают от тела. Например, в неравенстве (15-2) величине Q₂ следует приписать отрицательный знак, тогда оно приобретает такой вид:

,

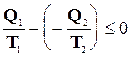или 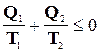. (15-3)

Аналогично, неравенство (15-2а) становится таким:

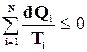. (15-3а)

Выражения (15-3) и (15-3а) известны как неравенства Клаузиуса. Следует отметить, что эти выражения становятся равенствами, если рассматриваемый цикл является обратимым, но они становятся строгими неравенствами, если хотя бы один из процессов, входящих в состав цикла, необратим.

Date: 2015-05-04; view: 624; Нарушение авторских прав