
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Теоремы Карно
|
|
Французским инженером С. Карно были исследованы различные циклы, по которым работают тепловые машины, и сформулированы некоторые общие принципы, касающиеся теоретически возможных КПД таких машин. Теперь эти принципы известны как теоремы Карно, которые гласят:
1. КПД всех обратимых тепловых машин, работающих с одним и тем же нагревателем и одним и тем же холодильником, одинаковы.
2. КПД необратимых тепловых машин, не может быть больше КПД обратимой машины, работающей с такими же нагревателем и холодильником, что и необратимая машина.
Для доказательства первого из этих положений рассмотрим две различные обратимые машины, КПД которых равны h1 и h2 соответственно. Не ограничивая об-
щности рассуждений, можно предположить, что обе машины, работая в прямом цикле, отбирают от нагревателя одно и то же количество теплоты21 Q1. Т.к. КПД машин разные, то холодильнику они отдают разные теплоты, величину которых
               нагреватель нагреватель
Q1 Q1
А2
обрат.машина А1 обрат.машина
прямой цикл орбат.цикл
Q2
нагреватель нагреватель
Q1 Q1
А2
обрат.машина А1 обрат.машина
прямой цикл орбат.цикл
Q2 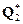 холодильник холодильник
Рис.57. К доказательству
теоремы Карно.
холодильник холодильник
Рис.57. К доказательству
теоремы Карно.

| обозначим Q2 и 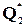 соответственно. КПД обеих машин определяются таким образом: соответственно. КПД обеих машин определяются таким образом:
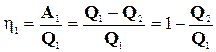 ; (14-5) ; (14-5)
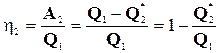 . (14-6)
Пусть h1> h2. Тогда А1 > А2 и Q2 < . (14-6)
Пусть h1> h2. Тогда А1 > А2 и Q2 < 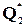 .Объеди-ним обе машины в один агрегат, где машина с большим КПД работает по прямому циклу, а другая по обратному, причем нагреватель и холодильник у .Объеди-ним обе машины в один агрегат, где машина с большим КПД работает по прямому циклу, а другая по обратному, причем нагреватель и холодильник у
|
них общие (см. рис 57). При совершении цикла в обратном направлении вторая обратимая машина отдает нагревателю такое же количество теплоты, которое она забирает у него при совершении прямого цикла. Кроме того, для работы второй машины по обратному циклу требуется работа внешних сил, равная по величине той работе, которую производит эта машина, работая по прямому циклу. При действии машин в агрегате работу внешних сил выполняет первая машина, затрачивая на это лишь часть своей работы, т.к. А1 > А2. После завершения цикла агрегата состояние нагревателя не изменилось, ибо он отдал первой машине теплоту Q1,
но такое же количество теплоты он получил от второй машины. Холодильник же получил теплоту Q2 от первой машины, но отдал второй машине 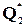 > Q2, т.е. он
> Q2, т.е. он
охладился. При этом агрегат произвел полезную работу А = А1 - А2. Таким образом видно, работа такого агрегата противоречит второму закону термодинамики в формулировке Томсона, и наше предположение о том, что h1> h2 неверно.
Нетрудно догадаться, что неверным является обратное предположение:h1<h2.
Для доказательства этого достаточно переномеровать машины (первая машина станет второй, а вторая - первой), тогда, повторяя только что проведенное рассуждение, получим требуемый результат. Поэтому остается только одна возможность: h1= h2, и первая теорема Карно доказана.
Доказательство второй теоремы проводится аналогично. Пусть КПД необратимой машины h1> h2, где h2 - КПД обратимой машины, имеющей общие с необратимой машиной нагреватель и холодильник. Поскольку в рассуждении доказательства первой части первой теоремы Карно обратимость или необратимость первой машины не играла никакой роли, то вывод о неправильности предположения о том, что h1> h2, где h1= hнеобрат сохраняет свою силу. Однако опровергнуть обратное предположение (hнеоб< hобр ), невозможно, т.к. необратимая машина не может работать по обратному циклу. Поэтому неравенство hнеоб< hобр остается справедливым, и вторая теорема Карно доказана.
Date: 2015-05-04; view: 816; Нарушение авторских прав