Закон Релея

Распределение таких существенно положительных величин, как эксцентриситет, биение, разностенность, непараллельность, неперпендикулярность, овальность, конусообразность, и некоторых других, характеризующихся их абсолютными значениями (т.е. без учета знака), подчиняется закону распределения эксцентриситета (закону Релея).

Распределение по закону Релея формируется, в частности, тогда, когда случайная величина R является радиус-вектором при двумерном гауссовом распределении, т.е. если она представляет собой геометрическую сумму двух случайных величин X и Y,

,

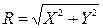каждая из которых подчиняется закону Гаусса с параметрами

L_Xср = L_Yср = L_Rср=0 и

σ_X = σ_Y = σ₀

Закон распределения Релея однопараметрический, и уравнение его кривой распределения имеет вид (см. рис.4)

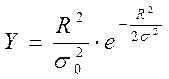, (1)

где σ₀ – среднее квадратическое отклонение значений координат X и Y.

Рис.4 Распределение размеров по закону Релея.

Уравнение (1) показывает, что при R=0 Y=0, т.е. начало кривой распределения совпадает с началом координат. Нисходящая ветвь этой кривой асимптотически приближается к оси абсцисс, так как при Y=0 R→∞.

Для теоретической кривой распределения по закону Релея (рис.4) характерны крутой подъем восходящей ветви и более пологий спуск нисходящей ветви. Вершина кривой более заострена, чем у кривой нормального распределения, и смещена от среднего значения переменной величины R в сторону начала координат.

Date: 2015-05-04; view: 1594; Нарушение авторских прав