Разложение логических функций по переменным. Совершенные нормальные формы

В данном разделе на примере булевых функций обсуждается понятие «нормальной формы», т.е. синтаксически однозначного способа записи формулы, реализующей заданную функцию.

Введем обозначения: 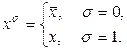(5.1)

Тогда: 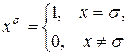, легко показать, . Обозначим: .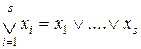

Теорема 5.1. Всякая логическая функция 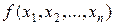может быть представлена в следующем виде:

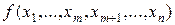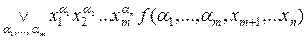= , (5.2)

где дизъюнкция берется по всем 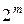наборам значений (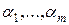) переменных , .

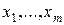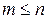Равенство (5.2) называется разложением функции f по переменным 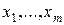. Например, при п = 4, т = 2 разложение имеет вид: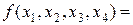

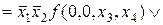
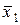
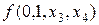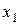
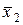
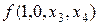Ú Ú .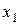

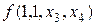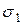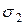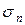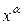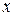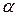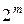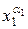
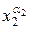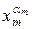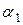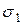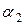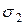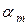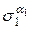
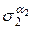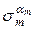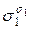
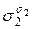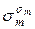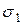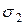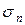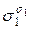
Доказательство. Теорема доказывается подстановкой в обе части равенства (5.2) произвольного набора значений (, ,…, , ,…, ) для всех переменных. Т.к. =1 только, когда = , то среди конъюнкций вида … отличны от нуля только те слагаемые, у которых = , = ,…, = . В этом случае … = … . Поэтому 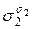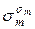f (, ,…, ) = … f (, ,…, , ,…, ) =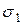

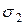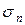= f (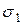, ,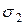…, , ,…, 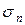), получили тождество. Ч.т.д.

При т =1 получаем разложение функции по первой переменной :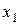

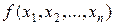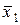
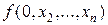= Ú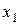

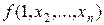
Разложение (5.2) можно строить по любому набору переменных, т.е. необязательно использовать первые т переменных. Разложение функции по переменной 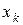имеет вид: =

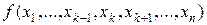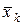
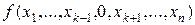= Ú .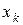

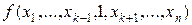Для логических формул введем понятия двух совершенных нормальных форм.

Определение 5.1. Элементарными конъюнкциями (дизъюнкциями) называются конъюнкции (дизъюнкции) переменных, в которых каждая переменная или ее отрицание встречается не более одного раза.

Определение 5.2. Конъюнктивной нормальной формой (КНФ) называется формула, имеющая вид конъюнкций элементарных дизъюнкций.

Определение 5.3. Дизъюнктивной нормальной формой (ДНФ) называется формула, имеющая вид дизъюнкций элементарных конъюнкций.

Рассмотрим разложение (5.2) по всем n - переменным (m=n). Тогда все переменные в правой части (5.2) получают фиксированные значения, а функции в конъюнкциях правой части становятся равными 0 или 1:

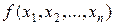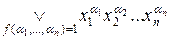= . (5.3)

Дизъюнкция берется по всем наборам (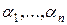), на которых f (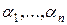) =1.

Такое разложение называется совершенной дизъюнктивной нормальной формой (СДНФ) функции f. СДНФ функции f содержит ровно столько элементарных конъюнкций, сколько единиц в таблице f. Каждому набору значений переменных (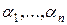), при котором f =1, соответствует элементарная конъюнкция всех переменных. Если 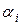= 0, то над переменной 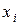ставится отрицание согласно соглашению (5.1). Если 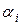=1, переменная 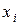используется без отрицания.

Теорема 5.2. Всякая булева функция (кроме 0) имеет единственную

СДНФ.

Теорема основывается на существовании взаимно однозначного соответствия между таблицей функции f и ее СДНФ. СДНФ определяется с точностью до порядка символов в конъюнкции и порядка следования конъюнкций. Единственная функция, не имеющая СДНФ - константа 0; 0 = .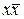

Введем совершенную конъюнктивную нормальную форму. Для этого рассмотрим СДНФ для отрицания функции f.

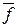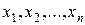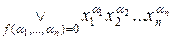() = , (5.4)

Здесь дизъюнкции берутся по всем наборам, на которых 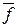=1, следовательно, f = 0. Возьмем отрицание от обеих частей равенства (5.4) и используем законы де Моргана. Тогда формула (5.4) примет вид конъюнкций элементарных дизъюнкций:

f (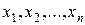) = 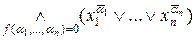. (5.5)

Полученной разложение называется совершенной конъюнктивной нормальной формой (СКНФ). Как и СДНФ, СКНФ определяется для каждой функции однозначно. Единственная функция, не имеющая СКНФ - константа 1.

Пример 5.1. Для импликации х® у записать СДНФ и СКНФ. Импликация задается таблицей:

Имеется три набора (0, 0), (0, 1), (1,1), на которых функция равна 1, поэтому СДНФ имеет вид дизъюнкции трех элементарных конъюнкций:

.

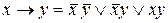Имеется один набор (1, 0), на котором импликация ложна, поэтому СКНФ имеет вид элементарной дизъюнкции:

.

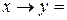
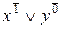
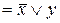Пример 5.2. Привести СДНФ и СКНФ функции , заданной таблицей:

Таблица 5.1

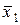
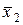
(, , ) = Ú Ú Ú ;

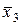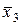(, , ) = ( Ú Ú 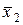) ( Ú Ú ) (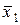 Ú Ú )( Ú Ú ).

Определение 5.4. Формулы, содержащие кроме переменных и скобок только знаки операций дизъюнкции, конъюнкции и отрицания, называются булевыми формулами.

СДНФ и СКНФ являются булевыми формулами, поэтому справедлива теорема:

Теорема 5.3. Всякая логическая функция может быть представлена булевой формулой.

Действительно, таким представлением может служить СДНФ, а 0 = .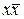

Под булевой алгеброй понимается алгебра, в которой логические операции состоят только из дизъюнкции, конъюнкции и отрицания.

Рассмотрим способ приведения булевых формул к ДНФ, который позволяют упростить исходную формулу. С помощью формулы двойного отрицания и законов де Моргана все отрицания «опускаются» до переменных. Затем раскрываются скобки. С помощью равенств (4.5) - (4.9) удаляются лишние конъюнкции, повторение переменных в конъюнкциях. С использованием свойств констант удаляются константы. Далее используются законы поглощения и склеивания.

Пример 5.3. Привести к ДНФ формулу : .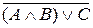

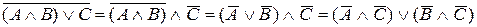Пример 5.4. Привести к ДНФ формулу :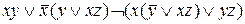

На первом этапе «опустим» все отрицания на переменные и получим:

= .

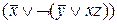
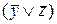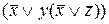
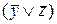На втором этапе раскроим скобки и проведем упрощения:

= = = = ;

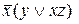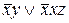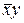
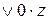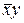
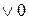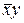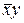
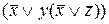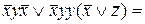
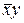= Ú = = ;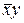

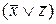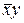
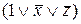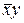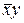
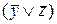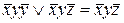= , используя закон 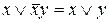, получаем:

= .

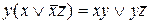Пример 5.5. Привести к ДНФ функцию , заданную таблицей 5.1.

Сначала запишем СДНФ для этой функции (см. пример 5.2):

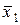
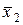
(, , ) = Ú Ú Ú =

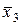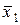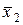
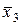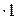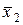
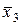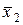
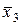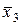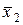
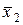
= ( Ú )Ú Ú = Ú Ú =

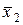
= Ú Ú = ( Ú )Ú = ( Ú )Ú =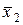

= Ú Ú = Ú ( Ú ) = Ú ( Ú ) = = Ú Ú .

Для булевой функции ДНФ не единственна.

Date: 2015-06-06; view: 1828; Нарушение авторских прав