
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

ОсНовные определения
|
|
Глава 1
ФУНКЦИИ АЛГЕБРЫ ЛОГИКИ
осНовные определения
Приведем определение логической функции от n переменных или булевой функции по имени Дж. Буля (1815 – 1864 г.г.). Буль впервые использовал алгебраические методы в логике, развивавшейся до его работ по преимуществу в рамках философии. Рассмотрим двухэлементное множество 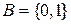 . Его элементы не являются числами в обычном смысле, 0 интерпретируется как «ложь» (F - «false», «нет»), 1- как «истина» (Т - «true», «да»). Пусть переменные
. Его элементы не являются числами в обычном смысле, 0 интерпретируется как «ложь» (F - «false», «нет»), 1- как «истина» (Т - «true», «да»). Пусть переменные 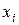 , 1£ i £ n, принимают значения из В.
, 1£ i £ n, принимают значения из В.
Определение 1.1. Функцией алгебры логики (логической функцией) от n переменных называется функция  , принимающая вместе со своими аргументами значения из В.
, принимающая вместе со своими аргументами значения из В.
Логическую функцию от n переменных называют также n- арной операцией на множестве В. Для логической функции одной переменной используют термин - унарная операция, а для функции двух переменных - бинарная операция.
Определение 1.2. Алгебра, образованная множеством В со всевозможными операциями на нем, называется алгеброй логики. Множество В называется основным или несущим множеством (носителем алгебры логики).
Обозначим  - множество всех булевых функций f от п переменных. Логическую функцию от п переменных можно задать таблицей истинности (Таблица 1.1). В последнем столбце
- множество всех булевых функций f от п переменных. Логическую функцию от п переменных можно задать таблицей истинности (Таблица 1.1). В последнем столбце  принимает значения 0 или 1. В таблице наборы значений для
принимает значения 0 или 1. В таблице наборы значений для  расположены по порядку возрастания соответствующих двоичных чисел. Такой порядок является общепринятым и позволяет задать логическую функцию набором её значений f = (
расположены по порядку возрастания соответствующих двоичных чисел. Такой порядок является общепринятым и позволяет задать логическую функцию набором её значений f = (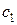 ,...,
,..., 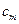 ), где
), где 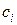 Î{0,1}, 1£ i £ m.
Î{0,1}, 1£ i £ m.
Таблица 1.1
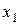 , …, , …, 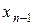 , , 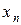
| 
|
| 0 … 0 0 0 … 0 1 … … … … 1 … 1 1 | 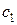 .
.
.
.
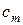
|
Например, если  = (00010111), то функция
= (00010111), то функция  зависит от 3 переменных и ей соответствует Таблица 1.2.
зависит от 3 переменных и ей соответствует Таблица 1.2.
Таблица 1. 2
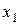
| 
| 
| 
|
Для логической функции от п переменных таблица истинности содержит m = 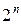 строк, соответствующих всем различным комбинациям значений переменных. Количество всех функций
строк, соответствующих всем различным комбинациям значений переменных. Количество всех функций  от п переменных равно числу различных столбцов таблицы 1.1, соответствующих наборам констант (
от п переменных равно числу различных столбцов таблицы 1.1, соответствующих наборам констант (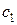 ,...,
,..., 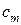 ). Это число совпадает с числом всех строк из 0 и 1 таблицы от m переменных, т.е. равно
). Это число совпадает с числом всех строк из 0 и 1 таблицы от m переменных, т.е. равно 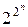 .
.
Пример 1.1. Рассмотрим задачу на построение булевой функции. Пусть три цеха  ,
,  и
и  снабжаются электроэнергией от электростанции, на которой установлены два генератора
снабжаются электроэнергией от электростанции, на которой установлены два генератора  и
и  , причем генератор
, причем генератор  обладает большей мощностью чем
обладает большей мощностью чем  . Если в энергии нуждается только один из цехов, то достаточно включить генератор
. Если в энергии нуждается только один из цехов, то достаточно включить генератор  , если же в энергии нуждаются одновременно два цеха -достаточно генератора
, если же в энергии нуждаются одновременно два цеха -достаточно генератора  . Снабжение энергией трех цехов обеспечивается совместной работой генераторов
. Снабжение энергией трех цехов обеспечивается совместной работой генераторов  и
и  . Необходимо описать работу логического устройства, которое бы анализировало заявки на электроэнергию от трех цехов и в зависимости от их потребности перераспределяло нагрузку между генераторами, включая или выключая по мере необходимости любой из них.
. Необходимо описать работу логического устройства, которое бы анализировало заявки на электроэнергию от трех цехов и в зависимости от их потребности перераспределяло нагрузку между генераторами, включая или выключая по мере необходимости любой из них.
Устройство должно иметь три выхода  ,
,  и
и  , каждый из которых может находиться в одном из двух состояний: «нуждаюсь в энергии» - 1 или «не нуждаюсь в энергии» - 0; и также должно иметь два выхода
, каждый из которых может находиться в одном из двух состояний: «нуждаюсь в энергии» - 1 или «не нуждаюсь в энергии» - 0; и также должно иметь два выхода  и
и  , через которые включаются (1) или отключаются (0) одноименные генераторы. Создание модели работы устройства состоит в построении логических функций
, через которые включаются (1) или отключаются (0) одноименные генераторы. Создание модели работы устройства состоит в построении логических функций  (
( ,
,  ,
,  ) и
) и  (
( ,
,  ,
,  ). Построим таблицу истинности для функций
). Построим таблицу истинности для функций  ,
,  .
.
Таблица 1.2

| 
| 
| 
| 
| |
| Ни один из цехов не нуждается в энергии, оба генератора выключены | |||||
| В энергии нуждаются только один или два цеха, включен один из генераторов, а другой выключен. | |||||
| В энергии нуждаются три цеха, включены оба генератора |
Логическая функция f Î  существенно зависит от переменной
существенно зависит от переменной 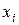 , если существует такой набор значений
, если существует такой набор значений 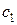 ,...,
,..., 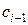 ,
, 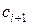 ,…,
,…, 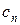 , что
, что
f (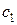 ,...,
,..., 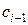 ,0,
,0, 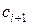 ,…,
,…, 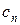 ) ¹ f (
) ¹ f (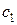 ,...,
,..., 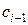 ,1,
,1, 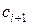 ,…,
,…, 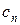 ).
).
В этом случае 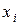 называется существенной переменной, в противном случае
называется существенной переменной, в противном случае 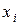 называют несущественной (фиктивной) переменной. Если
называют несущественной (фиктивной) переменной. Если 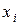 несущественная переменная f, то f (
несущественная переменная f, то f ( ,...,
,..., 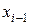 ,0,
,0, 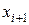 ,…,
,…, 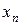 ) = f (
) = f ( ,...,
,..., 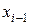 ,1,
,1, 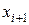 ,…,
,…, 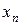 )
)
при любых значениях переменных  ,...,
,..., 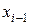 ,
, 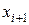 ,…,
,…, 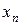 , и изменение значения
, и изменение значения 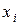 не меняет значения функции. Т.е.
не меняет значения функции. Т.е.  по существу зависит от (п -1)-переменной и представляет собой функцию
по существу зависит от (п -1)-переменной и представляет собой функцию 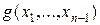 от (п- 1)- переменной. В этом случае говорят, что функция g получена из функции f удалением фиктивной переменной, а функция f получена из g введением фиктивной переменной. По определению булевы функции равны, если одна из другой получается введением (или удалением) фиктивных переменных. Смысл удаления фиктивных переменных очевиден, поскольку они не влияют на значения функции и являются с этой точки зрения лишними. Для общности рассуждений иногда полезно вводить фиктивные переменные для получения функций, зависящих от одного и того же количества переменных.
от (п- 1)- переменной. В этом случае говорят, что функция g получена из функции f удалением фиктивной переменной, а функция f получена из g введением фиктивной переменной. По определению булевы функции равны, если одна из другой получается введением (или удалением) фиктивных переменных. Смысл удаления фиктивных переменных очевиден, поскольку они не влияют на значения функции и являются с этой точки зрения лишними. Для общности рассуждений иногда полезно вводить фиктивные переменные для получения функций, зависящих от одного и того же количества переменных.
Пример 1. 2. Рассмотрим две функции  (
(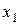 ,
,  ),
),  (
(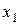 ,
,  ):
):
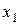
| 
| 
| 
|
Для функции  переменная
переменная 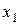 - существенная, т.к.
- существенная, т.к.  (0, 0) ¹
(0, 0) ¹  (1, 0), а переменная
(1, 0), а переменная  - несущественная:
- несущественная:  (0, 0) =
(0, 0) =  (0, 1),
(0, 1),  (1, 0) =
(1, 0) =  (1, 1). Легко убедиться, что для функции
(1, 1). Легко убедиться, что для функции  переменная
переменная 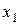 - несущественная, а
- несущественная, а  - существенная.
- существенная.
Date: 2015-06-06; view: 623; Нарушение авторских прав