Алгебра Жегалкина и линейные функции

Определение 9.1. Алгебра над множеством логических функций с двумя бинарными операциями Ù и Å называется алгеброй Жегалкина.

В алгебре Жегалкина выполняются соотношения:

x Å y = y Å x, x (y Å z) = xy Å xz, x Å x= 0, x Å 0 = x.

Отрицание и дизъюнкция выражаются следующим образом:

, x Ú y 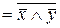=(x Å1)(y Å1) Å1= xy Å x Å y. (9.1)

Если в произвольной формуле алгебры Жегалкина раскрыть скобки и произвести всевозможные упрощения по выше перечисленным соотношениям, то получится формула, имеющая вид суммы по модулю 2 от логических произведений. Такая формула называется полиномом Жегалкина для данной функции. От булевой формулы всегда можно перейти к формуле алгебры Жегалкина и, следовательно, к полиному Жегалкина, используя равенства (9.1).

Рассмотрим примеры перехода от булевой функции к полиному Жегалкина.

Пример 9.1. (x Ú y) (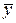 Ú xz) = (xy Å x Å y)( 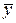xz Å 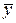Å x z) =

(x z (y Å1) Å (y Å1) Å xz) (xy Å x Å y)= (x y z Å x z Å y Å1 Å xz) (xy Å x Å y) =

=(x y z Å y Å1) (xy Å x Å y)= x y z Å x y z Å x y z Å x y Å x y Å y Å x y Å x Å y=

= x y z Å x y Å x.

Пример 9.2. xy Ú 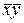= xy Å 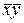(т.к. xy 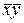=0) = xy Å(x Å1) (y Å1) =

= xy Å xy Å x Å y Å 1= x Å y Å 1.

Справедлива следующая теорема:

Теорема 9.1 Для всякой логической функции существует единственный полином Жегалкина.

Доказательство. Существование полинома уже доказано способом описания его построения. Для доказательства единственности найдем количество различных полиномов от п переменных. Число различных членов полинома (конъюнкций) от п переменных совпадает с количеством наборов значений для п переменных, которое равно 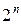. Число же различных полиномов, которые можно образовать из этих конъюнкций, равно 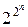и совпадает с количеством логических функций от п переменных. Т.к. разным функциям соответствуют разные полиномы, то тем самым между множеством функций и множеством полиномов от п переменных установлено взаимно однозначное соответствие. Это и доказывает единственность полинома Жегалкина для каждой функции.

Определение 9.2. Логическая функция f (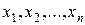), у которой полином Жегалкина имеет вид: 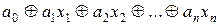, 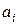Î{0,1}, 1£ i £ n,

называется линейным.

Все функции одной переменной линейны.

Пример 9.3. Найдем полином Жегалкина для эквивалентности и покажем ее линейность. Будем искать полином Жегалкина методом неопределенных коэффициентов:

x~ y =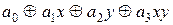

Рассмотрим таблицу истинности для ~:

При x = 0 y = 0 имеем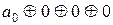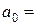: 1= , 1.

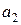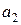При x = 0 y = 1 имеем: 0 = 1Å0 Å Å0, =1.

При x =1 y = 0 имеем: 0 = 1Å 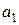Å 0Å 0, 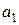=1.

При x =1 y =1 имеем: 1=1Å1Å1Å 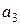, 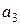=0.

Таким образом, x~ y = 1Å x Å y. Поэтому эквивалентность линейная функция.

Date: 2015-06-06; view: 1289; Нарушение авторских прав