
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Критерий функциональной полноты
|
|
Введем отношение £ для двоичных наборов длины п, составленных из 0 и 1. Для логических констант 0,1 будем считать: 0 £ 0, 1£ 1, 0 £ 1. Пусть s 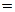 (
(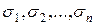 ), t
), t 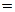 (
(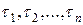 ), считается, что s £ t, если для всех 1£ i£ п выполняется
), считается, что s £ t, если для всех 1£ i£ п выполняется 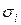 £
£ 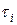 . Например, (0,1,0) £ (1,1,0), а наборы (0,1,0) и (1,0,1) несравнимы.
. Например, (0,1,0) £ (1,1,0), а наборы (0,1,0) и (1,0,1) несравнимы.
Определение 10.1. Логическая функция f (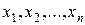 ) называется монотонной, если для любых двоичных наборов s
) называется монотонной, если для любых двоичных наборов s 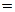 (
(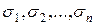 ), t
), t 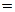 (
(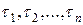 )
)
из s £ t следует, что f (s)£ f (t).
Пример 10.1. Константы 0, 1 и функция х -монотонны. Отрицание 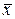 -
-
не монотонная функция.
Пример 10.2. Дизъюнкция и конъюнкция любого числа переменных являются монотонными функциями.
Пример 10.3. Функция  из Табл.1.2, является монотонной, а функция
из Табл.1.2, является монотонной, а функция  из этой же таблицы монотонной не является. Если бы функция
из этой же таблицы монотонной не является. Если бы функция  была монотонной, то на наборах (001) £ (101) должно выполняться неравенство
была монотонной, то на наборах (001) £ (101) должно выполняться неравенство  (001) £
(001) £  (101), однако
(101), однако  (001) =1,
(001) =1,  (101) = 0.
(101) = 0.
Для установления немонотонности логической функции достаточно найти хотя бы один набор, на котором не выполняется условие монотонности. Выяснение, является ли данная функция монотонной, требует рассмотрения достаточно большого числа наборов и для больших п оказывается трудоемкой. Приведем без доказательства критерий монотонности логических функций, который позволяет во многих случаях доказать монотонность функции, не прибегая к рассмотрению ее наборов.
Теорема 10.1 Всякая булева функция, не содержащая отрицания, представляет монотонную функцию, отличную от константы. Наоборот, для любой монотонной функции, не являющейся константой, найдется представляющая ее булева формула без отрицаний.
Пример 10.4. Докажем с помощью этой теоремы монотонность функции  , задаваемой в Табл.1.2. Ранее была построена в разделе 6 ДНФ для этой функции, которая имела вид:
, задаваемой в Табл.1.2. Ранее была построена в разделе 6 ДНФ для этой функции, которая имела вид:  (
( ,
,  ,
,  ) =
) = 
 Ú
Ú 
 Ú
Ú 
 . Данное представление является булевой формулой, не содержащей отрицания, следовательно
. Данное представление является булевой формулой, не содержащей отрицания, следовательно  - монотонна.
- монотонна.
Определение 10.2. Логическая функция f (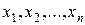 ) называется сохраняющей 0, если f (0, 0,…,0) = 0. Логическая функция f (
) называется сохраняющей 0, если f (0, 0,…,0) = 0. Логическая функция f (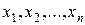 ) называется сохраняющей 1, если f (1,1,…,1) = 1.
) называется сохраняющей 1, если f (1,1,…,1) = 1.
Сформулируем критерий полноты Поста (без доказательства).
Теорема 10.2. (Критерий функциональной полноты). Для того чтобы система логических функций S была функционально полной, необходимо и достаточно чтобы она содержала: нелинейную функцию; немонотонную функцию; несамодвойственную функцию; функцию, не сохраняющую 0; функцию, не сохраняющую 1.
Пример 10.5. Доказать полноту системы логических функций
S= {  ~
~  ,
, 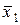 ,
, 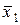 ®
® 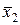 }.
}.
Решение. Функция 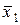 не является монотонной и не сохраняет 0, 1. Покажем, что ~ не является самодвойственной. Если бы это было так, то следующие две формулы были бы эквивалентны: Ø (
не является монотонной и не сохраняет 0, 1. Покажем, что ~ не является самодвойственной. Если бы это было так, то следующие две формулы были бы эквивалентны: Ø ( ~
~  ),
), 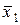 ~
~ 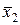 . Однако при
. Однако при
 =
=  первая формула равна 0, а вторая 1. Покажем, что среди рассматриваемых функций существует нелинейная. Отрицание и эквивалентность являются линейными функциями. Докажем нелинейность
первая формула равна 0, а вторая 1. Покажем, что среди рассматриваемых функций существует нелинейная. Отрицание и эквивалентность являются линейными функциями. Докажем нелинейность 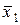 ®
® 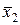 . Для этого найдем ее полином Жегалкина методом неопределенных коэффициентов.
. Для этого найдем ее полином Жегалкина методом неопределенных коэффициентов.
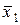 ®
® 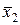 =
= 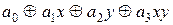 .
.
Построим таблицу истинности для 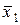 ®
® 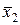 :
:

| 
| 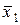
| 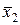
| 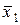 ® ® 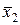 : :
|
Подставим в равенство поочередно различные наборы неизвестных.
При  = 0
= 0  = 0 имеем: 1=
= 0 имеем: 1= 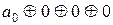 ,
, 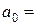 1.
1.
При  = 0
= 0  = 1 имеем: 0 = 1Å0 Å
= 1 имеем: 0 = 1Å0 Å 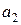 Å0,
Å0, 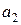 =1.
=1.
При  =1
=1  = 0 имеем: 1= 1Å
= 0 имеем: 1= 1Å 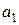 Å 0Å 0,
Å 0Å 0, 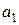 =0.
=0.
При  =1
=1  =1 имеем: 1=1Å0Å1Å
=1 имеем: 1=1Å0Å1Å 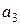 ,
, 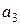 =1.
=1.
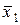 ®
® 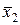 = 1Å
= 1Å  Å
Å 
 .
.
Система S - полная, согласно критерию функциональной полноты.
Date: 2015-06-06; view: 1049; Нарушение авторских прав