Сезонная и несезонная модели с трендом или без тренда

В дополнение к простому экспоненциальному сглаживанию, были предложены более сложные модели, включающие сезонную компоненту и тренд. Общая идея таких моделей состоит в том, что прогнозы вычисляются не только по предыдущим наблюдениям (как в простом экспоненциальном сглаживании), но и с некоторыми задержками, что позволяет независимо оценить тренд и сезонную составляющую. Gardner (1985) обсудил различные модели в терминах сезонности (отсутствует, аддитивная сезонность, мультипликативная) и тренда (отсутствует, линейный тренд, экспоненциальный, демпфированный).

Аддитивная и мультипликативная сезонность. Многие временные ряды имеют сезонные компоненты. Например, продажи игрушек имеют пики в ноябре, декабре и, возможно, летом, когда дети находятся на отдыхе. Эта периодичность имеет место каждый год. Однако относительный размер продаж может слегка изменяться из года в год. Таким образом, имеет смысл независимо экспоненциально сгладить сезонную компоненту с дополнительным параметром, обычно обозначаемым как d. Сезонные компоненты, по природе своей, могут быть аддитивными или мультипликативными. Например, в течение декабря продажи определенного вида игрушек увеличиваются на 1 миллион долларов каждый год. Для того чтобы учесть сезонное колебание, вы можете добавить в прогноз на каждый декабрь 1 миллион долларов (сверх соответствующего годового среднего). В этом случае сезонность – аддитивная. Альтернативно, пусть в декабре продажи увеличились на 40%, т. е. в 1.4 раза. Тогда, если общие продажи малы, то абсолютное (в долларах) увеличение продаж в декабре тоже относительно мало (процент роста константа). Если в целом продажи большие, то абсолютное (в долларах) увеличение продаж будет пропорционально больше. Снова, в этом случае продажи увеличатся в определенное число раз, и сезонность будет мультипликативной (в данном случае мультипликативная сезонная составляющая была бы равна 1.4). На графике различие между двумя видами сезонности состоит в том, что в аддитивной модели сезонные флуктуации не зависят от значений ряда, тогда как в мультипликативной модели величина сезонных флуктуаций зависит от значений временного ряда.

Параметр сезонного сглаживания d. В общем, прогноз на один шаг вперед вычисляется следующим образом (для моделей без тренда; для моделей с линейным и экспоненциальным трендом, тренд добавляется):

Аддитивная модель: .

Мультипликативная модель: .

В этой формуле 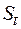обозначает (простое) экспоненциально сглаженное значение ряда в момент t, и 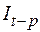обозначает сглаженный сезонный фактор в момент t минус p (p – длина сезона). Таким образом, в сравнении с простым экспоненциальным сглаживанием, прогноз «улучшается» добавлением или умножением сезонной компоненты. Эта компонента оценивается независимо с помощью простого экспоненциального сглаживания следующим образом:

Аддитивная модель: .

Мультипликативная модель: .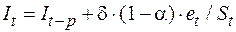

Обратите внимание, что предсказанная сезонная компонента в момент t вычисляется, как соответствующая компонента на последнем сезонном цикле плюс ошибка (, наблюдаемое минус прогнозируемое значение в момент t). Ясно, что параметр d принимает значения между 0 и 1. Если d = 0, то сезонная составляющая на следующем цикле та же, что и на предыдущем. Если d = 1, то сезонная составляющая «максимально» меняется на каждом шаге из-за соответствующей ошибки (множитель не рассматривается из-за краткости введения). В большинстве случаев, когда сезонность присутствует, оптимальное значение d лежит между 0 и 1.

Линейный, экспоненциальный, демпфированный тренд. Возвращаясь к примеру с игрушками, можно увидеть наличие линейного тренда (например, каждый год продажи увеличивались на 1 миллион), экспоненциального (например, каждый год продажи возрастают в 1.3 раза) или демпфированного тренда (в первом году продажи возросли на 1 миллион долларов; во втором увеличение составило только 80% по сравнению с предыдущим, т. е. на $800,000; в следующем году вновь увеличение было только на 80%, т. е. на $800,000 ´ 0.8 = $640,000 и т.д.). Каждый тип тренда по-своему проявляется в данных. В целом изменение тренда – медленное в течение времени, и опять (как и сезонную компоненту) имеет смысл экспоненциально сгладить его с отдельным параметром (обозначаемым g – для линейного и экспоненциального тренда, f – для демпфированного тренда).

Параметры сглаживания g (линейный и экспоненциальный тренд) и f (демпфированный тренд). Аналогично сезонной компоненте компонента тренда включается в процесс экспоненциального сглаживания. Сглаживание ее производится в каждый момент времени независимо от других компонент с соответствующими параметрами. Если g = 0, то тренд постоянен для всех значений временного ряда (и для всех прогнозов). Если g = 1, то тренд «максимально» определяется ошибками наблюдений. Параметр f учитывает, как сильно изменяется тренд, т. е. как быстро он «демпфируется» или, наоборот, возрастает.

Date: 2015-11-15; view: 523; Нарушение авторских прав